Funkcja, która każdej parze liczb naturalnych (i, j) dla 1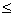 i
i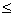 m oraz 1
m oraz 1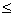 j
j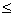 n przyporządkowuje jedną (dokładnie jedną) liczbę aij jest macierzą prostokątną o wymiarze m x n, co oznacza, że ma m wierszy i n kolumn.
n przyporządkowuje jedną (dokładnie jedną) liczbę aij jest macierzą prostokątną o wymiarze m x n, co oznacza, że ma m wierszy i n kolumn.
Macierz kwadratowa to taka macierz, która ma liczbę kolumn równą liczbie wierszy, czyli dla takiej macierzy m = n.
Dwie macierze są równe jeśli m = m', n = n' oraz aij = bij dla danych macierzy A i B.
Sumą macierzy A i B jest macierz C, której wyrazy są równe: cij = aij + bij. Dodawać macierze można tylko, jeżeli mają ten sam wymiar, czyli macierze dla których m = m' i n = n'
Iloczynem macierzy A i liczby D jest macierz B, której wyrazy są równe: B = DA, czyli B = Daij.
Różnicą macierzy A i B jest macierz C = A+(- B), gdzie - B jest iloczynem macierzy i liczby -1.
Iloczyn macierzy A i macierzy B jest macierz C, dla której cij = ai1b1j + ai2b2j + … + aipbpj
Mnożenie można wykonywać jedynie, jeśli liczba kolumn w macierzy pierwszej równa jest liczbie wierszy w macierzy drugiej.
Stąd macierz C = AB posiada tyle wierszy ile ma macierz A oraz kolumn ile ma macierz B.
Na ogół mnożenie nie jest przemienne.
Macierz transponowana do macierzy A = aij jest macierz AT = aji.
Macierz jednostkowa to macierz E kwadratowa stopnia n, której elementy aij = 0 jeżeli i 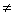 j oraz 1 jeżeli i = j.
j oraz 1 jeżeli i = j.
Macierzą diagonalną jest macierz kwadratowa, która posiada elementy niezerowe tylko na przekątnej.
Macierz kwadratowa stopnia n jest macierzą symetryczną jeśli A = AT.
Minor Mij stopnia n - 1 kwadratowej macierzy A, który odpowiada elementowi aij jest to wyznacznik macierzy stopnia n - 1, powstałej z macierzy A przez usunięcie wiersza o numerze i oraz kolumny o numerze j.
Wyznacznik macierzy A to suma iloczynów elementów w dowolnym wierszu przez ich algebraiczne dopełnienie przy ustalonym i oraz przy dowolnie j.
Macierz A jest osobliwa jeżeli ma wyznacznik różny od zero.
Macierz odwrotna do kwadratowej macierzy A to macierz A-1, która spełnia warunek AA-1 = A-1A = E.
Dla macierzy osobliwej A istnieje macierz odwrotna A-1, która jest określona wzorem A-1 = Ct/detA,
gdzie Ct jest macierzą dopełnień algebraicznych.
Funkcja F(x) jest funkcja pierwotna dla funkcji f(x) na danym przedziale X,
jeśli dla każdego x, który należy do X:
F'(x)=f(x).
Jeżeli F(x) jest funkcja pierwotna dla funkcji f(x) na danym przedziale X
to funkcja G(x) = F(x) +c, gdzie c to dowolna stała,
jest również funkcją pierwotną dla funkcji f(x) na przedziale X
Dla każdego x, który należy do X
G'(x) = [F(x) +c]' = F'(x) + 0 = f(x), dla każdego x, który należy do X
G'(x) = f(x)
Zbiór wszystkich funkcji pierwotnych dla funkcji f(x) na przedziale X nazywa się całką nieoznaczoną dla funkcji f(x), na przedziale X. Oznaczenie:
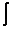 f(x)dx = F(x) + c
f(x)dx = F(x) + c
Jeśli funkcje f(x) i g(x) - całkowalne na przedziale (a, b) to f(x) +g(x) również całkowalne na przedziale (a, b).
Twierdzenie o całkowaniu przez części
Funkcje f(x) i g(x) na przedziale X mają pochodne ciągłe f'(x) i g'(X) wtedy:
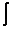
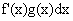 = f(x)g(x) -
= f(x)g(x) - 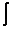
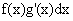 na przedziale X
na przedziale X
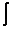
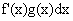 +
+ 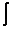
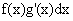 = f(x)g(x)
= f(x)g(x)
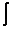 [f '(x) g(x) + f(x) g'(x)] dx = f(x) g(x)
[f '(x) g(x) + f(x) g'(x)] dx = f(x) g(x)
[f(x) g(x)]'= f '(x) g(x) + f(x) g'(x)
Twierdzenie o całkowaniu przez podstawianie
Jeśli funkcja t = h(x) ma pochodną h'(x), która jest ciągła na przedziale X oraz przekształca go w przedział T, a na przedziale T jest określona funkcja g(t), wtedy całka
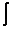 g[h(x)] h'(x)dx =
g[h(x)] h'(x)dx = 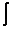 g(t) dt
g(t) dt
przy czym po obliczeniu 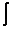 g(t) dt obowiązuje podstawienie t = h(x)
g(t) dt obowiązuje podstawienie t = h(x)
Jeśli funkcja jest ciągła oraz różniczkowalna i posiada w podanym punkcie ekstremum, to wtedy pochodna = 0
Jeśli funkcja jest ciągła oraz różniczkowalna to posiada w podanym punkcie ekstremum i może nie istnieć pochodna.
Jeśli funkcja jest ciągła, różniczkowalna i posiada punkt przegięcia to f ''(x) = 0
Funkcja jest wypukła ku górze, gdy dane otoczenie wykresu f ''(x) leży pod styczną f ''(x) < 0
Funkcja jest wypukła ku dołowi, gdy dane otoczenie wykresu f ''(x) leży nad styczną f''(x) > 0
Punkt x0 jest punktem przegięcia funkcji f jeśli funkcja f jest ciągła w pewnym otoczeniu punktu x0 oraz przy przejściu przez punkt x0 zmienia się charakter wypukłości.
Mówimy że funkcja f, która jest ciągła w przedziale (a, b) jest wypukła w górę (analogicznie w dół) w przedziale (a, b) jeśli w każdym punkcie przedziału )(a, b) jest wypukła w górę (w dół).
Asymptoty:
Pionowa - istnieje w punktach nieciągłości, albo na końcach dziedziny
Ukośna - jest wykresem funkcji y = ax + b, której współczynniki liczymy w następujący sposób:
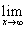 [f(x)/x] = a
[f(x)/x] = a
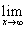 [f(x) -a x] =b
[f(x) -a x] =b
Pozioma - jeśli współczynnik a= 0
Reguła De Hospitala:
Jeśli f(x)/g(x) w punkcie x0 jest symbolem nieoznaczonym oraz f i g są określone, różniczkowalne w pewnym otoczeniu punktu x0, g'(x) 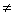 0 dla x należącego do tego otoczenia i istnieje granica właściwa
0 dla x należącego do tego otoczenia i istnieje granica właściwa 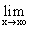 f'(x)g'(x)
f'(x)g'(x)
wtedy istnieje 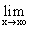 [f(x)/g(x)] oraz zachodzi
[f(x)/g(x)] oraz zachodzi 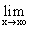 f(x)/g(x) = f '(x)
f(x)/g(x) = f '(x)


