Wiadomo powszechnie, że istnieją dwa rodzaje ładunków elektrycznych. Można to stwierdzić na podstawie zjawiska zwanego elektryzowaniem się ciał. Mianowicie jeśli pałeczka wykonana ze szkła zostanie potarta szmatką jedwabną i zbliżona do drugiej tak samo potraktowanej pałeczki szklanej to będzie można zauważyć , że będą się one nawzajem odpychać. Inny przykład to zachowanie się pałeczki plastikowej potartej futerkiem wobec pałeczki szklanej. Miedzy tymi pałeczkami obserwuje się przyciąganie. Natomiast dwie tak samo potraktowane pałeczki z plastiku będą się wzajemnie odpychały. Zjawisko to można wytłumaczyć faktem, że podczas pocierania na pałeczkach wytwarza się ładunek elektryczny. Ładunki zgromadzone na pałeczkach oddziałują ze sobą na dwa sposoby, stąd można wnioskować, że istnieją także dwa rodzaje ładunków. Fakt ten został odkryty przez Beniamina Franklina. Ładunkom gromadzącym się na szkle nadał on nazwę ładunków dodatnich, natomiast te gromadzące się na plastiku nazwał ładunkami ujemnymi. Wywnioskował, że ładunki które mają taką samą naturę będą się odpychały, natomiast ładunki różnoimienne będą się przyciągać.
Obecnie wiadomo, że materia w stanie obojętnym zawiera równe ilości ładunków dodatnich i ujemnych, tak więc ich suma jest równa zero. Natomiast podczas pocierania ładunki przepływają z jednego ciała na drugie i w ten sposób dochodzi do ładowania się ciał.
Ciała można podzielić na przewodniki i izolatory. I tak dobrymi przewodnikami są metale, ziemia czy ciało ludzkie. Natomiast do izolatorów należą szkło oraz tworzywa sztuczne. Izolatory inaczej nazywa się dielektrykami. Różnica między przewodnikami a izolatorami elektryczności jest taka, że w przewodnikach może następować swobodny przepływ ładunku natomiast w izolatorach dochodzi do unieruchomienia tych ładunków. Wyniki doświadczeń wskazują na to, że tak naprawdę ładunkami, które mogą się przemieszczać w przewodnikach są ładunki ze znakiem ujemnym czyli tzw. elektrony swobodne. Natomiast ładunki dodatnie zajmują stałe pozycje w metalu. W sytuacji gdy atomy łącza się i powstaje metal to elektrony zewnętrznych powłok oddzielają się i nie przynależą już do żadnego konkretnego atomu. Mogą się za to poruszać w obrębie całego metalu. Jeśli natomiast mamy do czynienie z przewodnikiem w stanie ciekłym, którym jest roztwór elektrolitu to w takim przewodniku obserwuje się ruchy zarówno ładunków ujemnych jak i dodatnich.
Po raz pierwszy siły występujące między dwoma ładunkami zmierzył i opisał w roku 1785 Charles Coulomb. Prawo przez niego sformułowane mówi, że pomiędzy dwoma ładunkami występuje siła wzajemnego oddziaływania , która można opisać następującą zależnością:
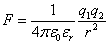
Analizując powyższy wzór widać , ze siła wzajemnego oddziaływania między ładunkami jest wprost proporcjonalna do iloczynu tych ładunków i odwrotnie proporcjonalna do kwadratu odległości między nimi. Pod tym względem prawo Coulomba przypomina prawo powszechnego ciążenia . Z ta tylko różnicą, że siły grawitacyjne mają zawsze charakter sił przyciągających natomiast w prawie Coulomba pojawiają się dwa rodzaje ładunków.
Pojawiający się we wzorze współczynnik 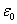 to przenikalność elektryczna próżni. Wynosi ona :
to przenikalność elektryczna próżni. Wynosi ona : 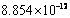
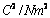 . Wartość oddziaływania między ładunkami zależy także od ośrodka, w którym się te ładunki znalazły. Dlatego we wzorze pojawia się jeszcze wielkość
. Wartość oddziaływania między ładunkami zależy także od ośrodka, w którym się te ładunki znalazły. Dlatego we wzorze pojawia się jeszcze wielkość 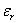 czyli względna przenikalność elektryczna ośrodka. I tak wartość przenikalności elektrycznej dla szkła wynosi 10, a dla wody 81.
czyli względna przenikalność elektryczna ośrodka. I tak wartość przenikalności elektrycznej dla szkła wynosi 10, a dla wody 81.
Jednostka ładunku elektrycznego jest w układzie SI określona na podstawie jednostki natężenia prądu elektrycznego. Jednostką ładunku jest jeden kulomb C i jest on równy ładunkowi, który płynie przez poprzeczny przekrój przewodnika w czasie 1 sekundy pod warunkiem ,że w przewodniku tym płynie prąd o natężeniu 1 ampera (A).
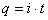
Równanie podane przez Coulomba dotyczy pary ładunków. Dlatego gdy w układzie występuje więcej ładunków dla każdej pary siłę oblicza się oddzielnie. I wtedy siłę wypadkową, która działa na jeden z tych ładunków oblicza się sumując wektorowo poszczególne siły dwuciałowe.
Gdy Franklin dokonywał rozróżnienia ładunku na dodatni i ujemny wtedy jeszcze nie zdawano sobie sprawy w jakiej postaci naprawdę występuje ładunek. Uważano ,że ma on formę płynu. Obecnie wiadomo, że całkowity ładunek danego ciała to nic innego jak wielokrotność minimalnego ładunku elektrycznego. Ładunek elementarny wynosi : 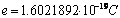 . Tak więc każdy ładunek występujący w przyrodzie można zapisać w postaci iloczynu
. Tak więc każdy ładunek występujący w przyrodzie można zapisać w postaci iloczynu 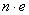 gdzie n jest liczbą całkowitą mogąca przybierać dodatnie lub ujemne wartości. Skoro więc istnieje pewna skończona "porcja" ładunku elektrycznego zatem jest on wielkością skwantowaną.
gdzie n jest liczbą całkowitą mogąca przybierać dodatnie lub ujemne wartości. Skoro więc istnieje pewna skończona "porcja" ładunku elektrycznego zatem jest on wielkością skwantowaną.
Jedną z podstawowych reguł fizyki jest zasada zachowania ładunku. Według tej zasady wypadkowy ładunek w układzie zamkniętym jest równy zero. Widać to chociażby na podstawie analizy opisanych wcześniej doświadczeń dotyczących zjawiska elektryzowania się ciał. W momencie gdy pręcik szklany pocierany jest szmatka jedwabną to pojawia się na nim ładunek dodatni. Na szmatce natomiast pojawia się natomiast identyczny co do wielkości ładunek ujemny. Tak więc nie dochodzi do wygenerowania ładunku elektrycznego , a jedynie do jego przepływu z jednego ciała do drugiego.
Ładunek elektryczny w otaczającej go przestrzeni wytwarza pole elektryczne, które oddziałuje na inne znajdujące się w sąsiedztwie ładunki. Widać więc, ze pole elektryczne jest pośrednikiem w przenoszeniu oddziaływań między ładunkami. Jeżeli w danym punkcie pola elektrycznego zostanie umieszczony ładunek próbny to natężenie pola elektrycznego w tym punkcie będzie równe stosunkowi siły działającej w tym punkcie na ładunek próbny do tego ładunku. Można to zapisać jako:
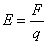
Natężenie pola elektrycznego jest wielkością wektorową, ponieważ wektorem jest siła a ładunek to wielkość skalarna. Kierunek wektora natężenia jest taki sam jak kierunek wektora siły. Odpowiada to kierunkowi ruchu ładunku dodatniego umieszczonego w tym punkcie pola. Kierunek pola E w przestrzeni może być przedstawiony graficznie za pomocą linii sił. Styczna do tych linii w każdym punkcie wyznacza kierunek wektora E w tym punkcie. Zależność pomiędzy liczbą linii sił a natężeniem pola jest taka, że liczba linii przypadająca na jednostkową powierzchnię jest proporcjonalna do wielkości natężenia pola. Widać więc, że jeśli w danym miejscu przestrzeni występuje duża koncentracja linii sił to natężenie w tym obszarze też ma dużą wartość. Początek linii sił jest zawsze na ładunkach dodatnich a koniec na ujemnych.
Inaczej wartość natężenia pola elektrycznego zapisać jako:
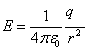
Aby znaleźć natężenie pola elektrycznego wytwarzanego przez kilka ładunków należy najpierw obliczyć wartość natężenia w danym punkcie pochodzącego od każdego z ładunków. Następnie należy przeprowadzić operację sumowania wektorowego tych natężeń po wszystkich ładunkach.
Jeśli mamy do czynienia z ciągłym rozkładem ładunków wówczas natężenie pola w danym punkcie można obliczyć dzieląc ładunek na nieskończenie małe elementy dq. Każdy taki element należy potraktować jako ładunek punktowy i obliczyć od niego natężenie w danym punkcie. Można zapisać, że:
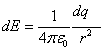
Ostatnim krokiem będzie znalezienie wypadkowego pola w tym punkcie . W tym celu należy przeprowadzić operację całkowania po wszystkich elementach dE. Otrzymujemy więc:
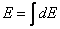
Pole elektryczne oddziałuje na cząstkę naładowaną z siła równą:
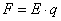
Tak więc siła ta nadaje cząstce przyspieszenie zgodnie z zależnością:
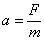
gdzie m to masa cząstki.
Jeżeli dwa ładunki elektryczne różnoimienne zostaną umieszczone w stałej odległości przyjętej jako 2a to układ taki nazywa się dipolem elektrycznym. I teraz jeżeli taki dipol zostanie umieszczony w jednorodnym zewnętrznym polu elektrycznym to na ten dipol zaczną działać dwie równe co do wartości ale przeciwnie skierowane siły. Stąd wypadkowa siła działająca na ten dipol jest równa zeru. Jednak na układ działa niezerowy wypadkowy moment obracający ten dipol . Oś obrotu przechodzi przez punkt znajdujący się w środku odcinka łączącego oba ładunki. Ten moment można przedstawić jako:
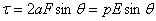
gdzie kąt 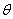 to kąt zawarty między momentem dipolowym p, a wektorem natężenia pola elektrycznego E.
to kąt zawarty między momentem dipolowym p, a wektorem natężenia pola elektrycznego E.
Można więc powiedzieć, że w zewnętrznym polu elektrycznym dipol poddany jest działaniu momentu skręcającego , który dąży do ustawienia tego dipola wzdłuż linii pola.
Moment skręcający można przedstawić jako:
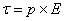
Kolejną wielkością dotyczącą pola elektrycznego jest strumień pola elektrycznego. Jest to iloczyn skalarny wektora powierzchni S oraz wektora natężenia pola elektrycznego E.
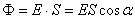
Kąt alfa jest kątem zawartym między tymi dwoma wektorami.
Istnieje prawo podające związek między strumieniem pola elektrycznego przechodzącego przez dana powierzchnię i całkowitym ładunkiem zgromadzonym na tej powierzchni. Jest to prawo Gaussa dla elektryczności. Ma ono postać:
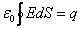
Prawo to może być stosowane zarówno do wyznaczania natężenia pola jak i do obliczania całkowitego ładunku.


