Fale , które rozchodzą się w ośrodkach sprężystych noszą nazwę fal mechanicznych. Przykładem takich fal mogą być fale dźwiękowe. Do powstania takich fal dochodzi wskutek wychylenia się fragmentu danego ośrodka sprężystego z położenia równowagi. W konsekwencji dochodzi do drgań tej cząstki bądź atomu wokół położenia równowagi. Te drgania następnie rozprzestrzeniają się na dalsze fragmenty ośrodka właśnie dzięki jego własnościom sprężystym. Tak rozchodzi się w ośrodku zaburzenie czyli fala mechaniczna. Należy jeszcze dodać, że ośrodek materialny jako całość nie wykonuje ruchu, chodzi tutaj tylko o ruch drgający jego poszczególnych fragmentów. Ruch fali to ruch jednostajny.
Ruchem falowym więc nazywa się rozprzestrzenianie się zaburzenia w ośrodku materialnym.
Fala, która dobiega do danego punktu w ośrodku materialnym przekazuje mu energię. Na energię fali składa się energia kinetyczna i potencjalna cząstek materii. Energia może być zatem przekazywana przez fale na duże odległości a jej przenoszenie polega na przekazywaniu jej kolejno na coraz dalsze fragmenty ośrodka materialnego.
Fale mechaniczne przenoszą więc energię dzięki przesuwaniu się zaburzenia w ośrodku a nie dzięki ruchowi całego ośrodka.
Fale można podzielić ze względu na kilka cech. Jedna z klasyfikacji bierze pod uwagę kierunek drgań cząstek ośrodka względem kierunku propagacji fali. I tak fale dzieli się na :
- fale podłużne - cząstki drgają wzdłuż kierunku rozchodzenia się fali, przykład stanowić mogą fale dźwiękowe w powietrzu,
- fale poprzeczne - cząstki drgają w kierunku poprzecznym do kierunku rozchodzenia się fali
Ze względu na rodzaj zaburzenia fale można podzielić m.in. na :
- fale harmoniczne - powstające w wyniku drgań harmonicznych źródła
- impulsy falowe - źródłem takiej fali jest jednorazowe zaburzenie w ośrodku materialnym.
Jeżeli dla dowolnej fali periodycznej połączy się punkty o takiej samej fazie drgań to powierzchnie taką nazywa się czołem fali lub powierzchnia falową. Jeśli fala taka rozchodzi się w ośrodku izotropowym i jednorodnym to kierunek rozchodzenia się tej fali jest zawsze prostopadły do powierzchni falowej.
Natomiast każda prosta, która jest prostopadła do czoła fali i ma kierunek fali nosi nazwę promienia fali.
W zależności od kształtu czoła fali fale można podzielić na:
* fale płaskie - czoła fali są płaszczyznami, a promienie liniami prostymi wzajemnie równoległymi.
* fale kuliste - czoła fali są kulami, a promienie rozchodzą się ze źródła we wszystkich kierunkach.
Rozchodzenie się fal w przestrzeni najlepiej jest omówić na najprostszym przypadku. Należy więc przyjąć założenie, że mamy do czynienia z falą poprzeczna , która rozchodzi się wzdłuż naprężonego sznura . Jako kierunek propagacji fali przyjmijmy x.
W chwili początkowej kształt sznura można opisać równaniem: y= f(x), gdzie y oznacza poprzeczne wychylenie sznura. Następnie analizujemy co dzieje się w przeciągu czasu t. A mianowicie w tym czasie fala przemieszcza się w kierunku x z prędkością v wzdłuż sznura. Po odcinku czasu t początkowe równanie przyjmie teraz postać:
y = f ( x - vt )
Jeżeli przyjmiemy teraz, że fala rozchodząca się wzdłuż sznura jest falą harmoniczną to w chwili początkowej równanie będzie wyglądało następująco:

W powyższym równaniu jako A oznaczono amplitudę czyli maksymalne wychylenie sznura, natomiast 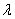 to długość fali. Jest ona równa odległość między punktami, które mają taką samą fazę.
to długość fali. Jest ona równa odległość między punktami, które mają taką samą fazę.
Natomiast po czasie t , jeśli fala biegnie w kierunku dodatnim, czyli w prawo równanie przyjmuje postać:

Stosunek długości fali do prędkości nosi nazwę okresu fali. Wyznacza on czas, w którym fala pokonuje
odległość równa długości fali.

Zatem po podstawieniu powyższej zależności do wzoru na wychylenie po czasie t otrzymujemy:

Należy wprowadzić jeszcze inne wielkości dotyczące fali. I tak liczbę falowa definiuje się jako:

a częstość kołową jako:

gdzie 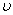 to częstość fali.
to częstość fali.
Wykorzystując te dwie wielkości równanie fali biegnącej można przedstawić jako:

A prędkość fali można wyrazić jako:

Prędkość fali zależy od sprężystości i bezwładności danego ośrodka materialnego.
Fale biegnące w przestrzeni pokonują dany fragment ośrodka materialnego niezależnie od siebie. Tak więc wypadkowe przemieszczenie danej cząstki ośrodka jest równe wektorowej sumie przemieszczeń pochodzących od poszczególnych fal. Jest to tzw. zasada superpozycji. Jeżeli dojdzie do nałożenia się dwóch lub więcej ciągów falowych, to mówi się o tzw. zjawisku interferencji.
Dotychczas rozpatrywane równania dotyczyły fali biegnącej w kierunku dodatnim. Jeśli fala będzie się rozchodziła w kierunku ujemnym to równanie przyjmie postać:

Fala taka może powstać w wyniku odbicia fali biegnącej w kierunku dodatnim od granicy ośrodków. Jeśli dojdzie do nałożenia się takich fal to równanie fali wypadkowej przyjmie postać:

Jest to tzw. fala stojąca. Punkty, w których amplituda takiej fali jest maksymalna nazywa się strzałkami fali, a punkty z minimalna amplitudą to węzły fali. Dla tej fali charakterystyczny jest fakt, że energia nie może być przez nią transportowana. Mianowicie przeszkodę stanowią węzły. Czyli dochodzi do trwałego zmagazynowania energii w danych punktach ośrodka.
Dla fali stojącej charakterystyczne jest to, że amplituda dla różnych cząstek nie jest taka sama, ale ulega zmianie wraz z położeniem cząstki.
Jeżeli układ , który jest zdolny do wykonywania drgań zostanie pobudzony impulsami o częstości równej lub zbliżonej do częstości jego drgań własnych to zostaje wprawiony w drgania o dużej amplitudzie. Określa się to jako rezonans.
I tak jeśli np. będzie my dalej rozpatrywać analizowany wcześniej sznur tym razem zamocowany na obu końcach to można wywołać w takim układzie powstanie fali stojącej. Odległość między sąsiednimi węzłami jest równa:

gdzie l to długość sznura.
Stąd wynika ,że :

Dodatkowo wiadomo, że:
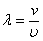 , a
, a 
gdzie F to naprężenie liny a 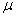 to tzw. gęstość jednostkowa czyli masa przypadająca na jednostkę długości liny.
to tzw. gęstość jednostkowa czyli masa przypadająca na jednostkę długości liny.
Otrzymujemy zatem:

Jeżeli teraz częstość wymuszająca jest równa jednej z częstości własnych sznura, będzie on drgał z tą częstością i z dużą amplitudą.
Na koniec warto wspomnieć jeszcze o jednym zjawisku, a mianowicie o efekcie Dopplera.
Zjawisko to dotyczy wszystkich fal, ale najlepiej można je zobrazować na przykładzie fali dźwiękowej. Jeżeli źródło dźwięku znajduje się w spoczynku i emituje dźwięki o długości fali 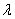 . Fale te rozchodzą się z prędkością v. I jeśli obserwator jest nieruchomy to po danym czasie t dociera do niego vt /
. Fale te rozchodzą się z prędkością v. I jeśli obserwator jest nieruchomy to po danym czasie t dociera do niego vt / 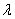 fal. Jeśli jednak obserwator porusza się w kierunku źródła dźwięku z prędkością v
fal. Jeśli jednak obserwator porusza się w kierunku źródła dźwięku z prędkością v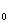 to dociera jeszcze do niego dodatkowo v
to dociera jeszcze do niego dodatkowo v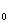 t/
t/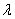 fal. Tak więc obserwator będzie słyszał dźwięki o częstotliwości wyższej niż częstotliwość źródła. Można to wyrazić zależnością:
fal. Tak więc obserwator będzie słyszał dźwięki o częstotliwości wyższej niż częstotliwość źródła. Można to wyrazić zależnością:

Identyczna sytuacja będzie miała miejsce, gdy to źródło będzie się zbliżało do obserwatora. Jeśli jednak zajdzie wzajemne względne zwiększanie odległości między źródłem i obserwatorem to słyszana częstotliwość będzie niższa od częstotliwości źródła.

Taki efekt każdy z nas obserwował wielokrotnie chociażby na przykładzie zmiany częstotliwości klaksonu samochodu, który przejeżdżał koło nas lub sygnału karetki pogotowia.


