1. Momenty żyroskopowe
  2. Pola potencjalne
  3. Oddziaływania potencjalne
  4. Galileuszowska zasada względności
  5. Transformacja Lorentza
  6. Interwał czasoprzestrzenny
  7. Kinematyka w Szczególnej Teorii Względności
  8. Dynamika w Szczególnej Teorii Względności
  9. Siły bezwładności
  10. Bezwładność i grawitacja
  11. Równoważność masy grawitacyjnej i bezwładnościowej - konsekwencje
  12. Odwracalność i nieodwracalność procesów
  13. Entropia
  14. Zasada ekwipartycji
  15. Tłumione drgania swobodne
  16. Oscylator harmoniczny tłumiony z siłą wymuszającą
  17. Rezonatory
  18. Fale
  19. Energia fali
  20. Interferencja fal
  21. Paczka falowa
  22. Interferencja fal pochodzących ze źródeł punktowych
  23. Zasada Huyghensa
  24. Dyfrakcja fali na obiektach rzeczywistych
  25. Holografia
  26. Charakterystyki kierunkowe odbiorników i nadajników
  27. Zachowanie się fali na granicy ośrodków
  28. Fale stojące
  29. Pole elektryczne - indukcja, natężenie i potencjał.
  30. Prawo Gaussa
  31. Elektryczny dipol
  32. Pole magnetyczne - natężenie i indukcja
  33. Prawo Ampere'a
  34. Cząstka o określonym ładunku poruszająca się w polu magnetycznym
  35. Dipol magnetyczny
  36. Prawa indukcji Faradaya. Równania Maxwella
  37. Zastosowanie indukcji elektromagnetycznej
  38. Równania Maxwella
  39. Promieniujący dipol elektryczny
  40. Obwód elektryczny emitujący falę elektromagnetyczną
  41. Antena dipolowa
  42. Światło spójne i niespójne
  43. Interferencja światła niespójnego
  44. Luneta
  45. Fale de Broglie'a
  46. Równanie Schrodingera
  47. Zasada nieoznaczoności Heisenberga
  48. Cząstka w stanie związanym
  49. Promieniowanie Roentgena
  50. Stan układów termodynamicznych
  51. Ruch cieplny
  52. Rozpad B
  53. Rozszczepienie jądrowe
  54. Reaktor jądrowy

1. Momenty żyroskopowe

Zasada działania żyroskopu - mamy obracające się ciało, które posiada moment pędu J. Ciało to znajduje się w polu siły F, która powoduje powstanie momentu siły M, działającego na obracające się ciało. II zasada dynamiki Newtona dla układów obracających się, mówi że działanie momentu siły na ciało powoduje zmianę jego momentu pędu. Tak więc moment siły M, powoduje zmianę momentu pędu o dK, w czasie dt. Kierunek wektora dK, jest zgodny z kierunkiem działania wektora M, czyli prostopadle do wektora K. Tak więc momentu pędu zostanie zmieniony w sposób nieznaczny i wynosi teraz K + dK, czyli w przybliżeniu jego długość jest taka sama, natomiast zmienił się tylko jego kierunek, a mianowicie został obrócony o kąt dφ = dK/K. W ten sposób działając momentem siły o kierunku prostopadłym do kierunku momentu pędu powodujemy obrót osi wokół której ciało rotuje. Możemy obliczyć jaka jest prędkość kątowa obrotu osi, która jest określana mianem prędkości kątowej precesji ω.

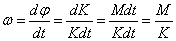
Stąd znając prędkość kątową precesji, możemy obliczyć, jaki moment siły działa na ciało będące w polu określonej siły:

M=ωK

Jest to tzw. moment sił żyroskopowych, który równoważy momenty sił powstający podczas precesji bąka.

Najprostszym przykładem bąka jest zabawka dla dzieci, ale zasada jego działania jest też wykorzystywana podczas jazdy na rowerze, a także w wyspecjalizowanych żyroskopach służących do nawigacji.

2. Pola potencjalne.

Zakładamy, że mamy dwa ciała, z których jedno umieszczamy w początku układu współrzędnych, a rozpatrujemy zachowanie się ciała drugiego. Możemy teraz obserwować jak obecność jednego ciała wpływa na zachowanie drugiego. Otóż jeśli zauważymy, że ciało to przemieści się z położenia w punkcie 1 do położenia w punkcie 2, a przy tym przebędzie odcinek drogi o długości dl, to możemy powiedzieć, że praca jaka została wykonana wynosi

dW = Fdl = F1dl= U(1) - U(2) = -dU

gdzie dU oznacza zmianę energii potencjalnej, jakiej ciało doznało przy przejściu z punktu 1 do punktu 2. W tym wypadku praca jest niezerowa, jeśli niezerowa jest składowa F1 równoległa do kierunku przesunięcia dl. Korzystając z tego możemy określić, jaki jest związek pomiędzy zmianą energii potencjalnej, a działającą siłą:

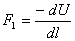
Widzimy więc, w ten sposób, że zawsze możemy określić siłę działająca na ciało, jeśli tylko znamy rozkład energii potencjalnej U(r), czyli znamy pole w jakim znajduje się nasze ciało. W przypadku gdy wartość energii potencjalnej, drastycznie maleje, gdy oba ciała oddalamy od siebie na bardzo dużą odległość, możemy się spodziewać, że przy zwiększeniu ich odległości do nieskończoności, wartość energii potencjalnej zmalałaby do zera. Jednak dzięki temu, jesteśmy w stanie dokładnie określić związek pomiędzy siłą z jaką oba ciała na siebie oddziałują, a energią tego oddziaływania. Praca jaką wykonuje siła działająca na ciało, która pozwala na jego przesunięcie z odległości R do nieskończoności - ¥ wynosi:

W = Fdr = U(R) - U(¥) = U(R)

Korzystając dodatkowo z tego, iż każdy wektor możemy rozłożyć na sumę składowych:

F = Fxi + Fyj + Fzk

Otrzymujemy wyrażenie na siłę F działającą na ciało znajdujące się w polu U:

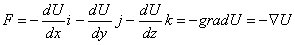
Wielkość pola można obrazowo zilustrować za pomocą linii sił pola. O tym jak pole w danym miejscu jest silne, czyli jak duża siła działa na ciało w tym miejscu, określa gęstość tych linii. Dodatkowo mają one taki kształt, że w każdym punkcie siła jaka działa na ciało ma kierunek styczny do tych linii. Rozpatrując powierzchnie prostopadłe do kierunku linii sił pola, można zauważyć, że praca wykonana w tym polu będzie równa zero. Takie powierzchnie nazywa się powierzchniami ekwipotencjalnymi, co znaczy tyle samo co stwierdzenie, że utrzymuje się na nich stała wartość potencjału. Skoro wykonana praca jest równa zero, to oznacza, że energia potencjalna ciała na takiej powierzchni się nie zmienia. W fizyce mamy do czynienia z różnymi typami pół, dla przykładu weźmy pola grawitacyjne i elektryczne. Są one dobrze sprecyzowane i opisane. W każdym z tych pół to jakiego działania siły doznaje dane ciało zależy bezpośrednio od jego własności od tego jaką ma masę, lub jaki posiada ładunek. Parametr ten jest zawsze charakterystyczny dla danego ciała i można go określić jako nabój C ciała. Dzięki temu możemy sformułować wyrażenie na natężenie pola i jego potencjał, które są odpowiedzialne za siły działające na dane ciało.

Natężenie pola określa się przez wyrażenie:

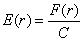
Natomiast potencjał pola jako:

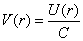
Wielkości te spełniają wzajemną relację:

E = -grad V

Nie należy uważać, że pojęcie pola jest czystą abstrakcją, jest to jak najbardziej rzeczywista wielkość. Doświadczenia tego dowodzą, jeśli w przestrzeni umieści się określone ciało, obdarzone masą bądź ładunkiem elektrycznym, to rzeczywiście powoduje ono zmianę otaczającej go przestrzeni.

3. Oddziaływania potencjalne

Oddziaływania jakie towarzyszą ciału znajdującemu się w danym polu mają określone podstawowe właściwości:

  • Siła z jaką oddziałują na siebie ciała bezpośrednio zależy od odległości między nimi, a w przypadku gdy ta odległość zmierza do nieskończoności, wartość siły zmierza do zera: F(¥) = 0.
  • Praca wykonana przez siły pochodzące od pola potencjalnego, gdy jest wykonana po drodze zamkniętej wynosi 0. Wniosek ten wynika bezpośrednio z tego, iż praca wykonana w takim polu zależy tylko od bezpośredniej odległości pomiędzy punktami określającymi przemieszczenie ciała, a nie od drogi po której to ciało się poruszało. Wskutek wykonania pracy przez silę pochodzącą od oddziaływania maleje wartość energii tegoż oddziaływania. Stąd można dalej wywnioskować, że każdemu wzajemnemu położeniu ciał, każdemu układowi ciał, odpowiada określona wartość energii oddziaływania - U. Tak określoną energię oddziaływania nazywamy energią potencjalną ciała, a z kolei oddziaływani to nazywamy oddziaływaniem potencjalnym, bądź zachowawczym. W fizyce istnieje kilka oddziaływań potencjalnych, a najważniejsze z nich to oddziaływanie grawitacyjne i oddziaływanie kulombowskie. Siła oddziaływania grawitacyjnego pomiędzy dwom ciałami zależy od ich mas, a także od ich wzajemnej odległości:

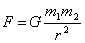
Energia oddziaływania grawitacyjnego wynosi:

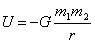
W przypadku oddziaływania kulombowskiego siła jaka działa na dwa ładunki wynosi:

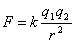
A energia oddziaływania dla tego pola:

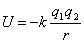
Istnieją jeszcze inne rodzaje oddziaływań, takie jak oddziaływania Van der Waalsa, które dokładnie opisują zachowanie się cząsteczek w gazie, a także oddziaływania jakich doznają atomy znajdujące się kryształach będą wtedy w tzw. potencjale Morse'a.

4. Galileuszowska zasada względności

Została sformułowana w 1632 roku i ukazywała zasadniczy pogląd na otaczający nasz świat. Jej główne wnioski można opisać poprzez eksperyment myślowy. Otóż wyobraźmy sobie, że podróżujemy w zamkniętym pomieszczeniu, np. w kajucie na statku. Mam szczęście i nasz statek, płynie po niczym niezmąconej wodzie. W naszej kajucie mamy różne przedmioty, jakieś rośliny, a nawet przyrządy pomiarowe. Otóż według Galileusza, przeprowadzając wszelkie możliwe doświadczenia, będąc zamkniętymi w kajucie, nie możemy w żaden sposób wywnioskować, czy nasz statek się porusza, czy też stoi nieruchomo. W fizyce układ podobny naszej wymyślonej kajucie nazywa się układem inercjalnym. We wszystkich układach inercjalnych, które mogą się poruszać względem siebie ze stałymi prędkościami, wszystkie prawa przyrody są takie same. Wydaje się to dosyć naturalne, że prawa przyrody, rządzące zjawiskami fizycznymi powinny być takie same przy przejściu do innego układu, ponieważ w innym przypadku mogłyby powstać bardzo dziwne paradoksy. Wniosek ten jest określany, jako niezmienniczość praw przyrody, względem dowolnego układu inercjalnego. Jednak aby przekazać swoje obserwacje mierzone w jednym układzie inercjalnym do drugiego układu inercjalnego, należy się posłużyć pewną transformacją, mającą na celu przeliczenie odpowiednich wartości położenia i czasu do nowego układu. Do tego celu posłużymy się dwoma układami, pierwszym oznaczonym przez współrzędne x,y i z, oraz drugim, który oznaczamy przez współrzędne x', y' i z'. Dodatkowo zakładamy, że układ "primowany" = O' porusza się względem układu "nieprimowanego" - O z pewną stałą określoną prędkością v. Załóżmy także, że układ ten porusza się zgodnie z dodatnim kierunkiem wartości osi x. Kolejne założenie dotyczy pomiaru czasu i mówi o tym, że czas rozpoczęto mierzyć w każdym układzie z chwilą, gdy początek układu O' pokrywał się z początkiem układu O. Dochodzimy teraz do sedna transformacji Galileusza. Otóż jeśli obserwator znajdujący się w układzie O zanotował, że ciało w chwili czasu t, znajdowało się w punkcie o współrzędnych x, y i z. To według obserwatora znajdującego się w układzie O', ciało to w chwili t'=t, znajdowało się w punkcie o współrzędnych x' = x-vt, y'=y, z'=z. Transformacja Galileusza, do tej pory z powodzeniem opisuje wiele zjawisk z naszego życia codziennego. Wiele także zjawisk jest niezmienniczych względem transformacji Galileusza. Tak jest w przypadku zasady zachowania pędu, która opisuje, co się dzieje z pędem układu ciał przed określonym zdarzeniem i po nim. Pęd ten mianowicie pozostaje zachowany. Jak wiemy pęd wyraża się jako iloczyn masy i prędkości ciała. Jeżeli obliczymy zasadę zachowania pędu dla układu dwóch ciał zderzających się w układzie O, to otrzymamy:

m1v1 + m2v2 = m1u1 + m2u2

Przy przejściu z tą zasadą zachowania pędu do układu O', po obu stronach powyższego wyrażenia pojawi się czynnik związany z prędkością układu O' względem układu O. Czynnik ten, jako że będzie identyczny po obu stronach, może natychmiast zostać zredukowany, w ten sposób pokazując nam że całkowity pęd się nie zmienił przy przejściu z jednego układu do drugiego. Innymi wielkościami które są niezmiennicze względem transformacji Galileusza to energia, a także temperatura.

5. Transformacja Lorentza.

Otóż transformacja Galileusza okazała się w swojej istocie błędna. Można ją stosować, do zjawisk z naszego życia codziennego, jednak dla przypadków gdy w grę wchodzą już większe prędkości układów, takie które można porównywać z wartością prędkości światła, należy stosować transformację Lorenta.

Według tejże transformacji współrzędne mierzone w układzie O' przyjmują wartości:

gdzie: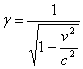

Transforamacja ta prowadziła do wniosków zupełnie nie osiągalnych dla mechaniki klasycznej. Została ona ogłoszona przez Lorentza w 1899, a w 1905 roku Einstein użył jej do sformułowania swojej przełomowej Szczególnej Teorii Względności. W teorii tej założył, że prędkość światła jest wszędzie taka sama, bez względu na to w jakim układzie jest mierzona.

6. Interwał czasoprzestrzenny.

Interwał, ten określa jednoczesność zdarzeń. Jego istotę można wyjaśnić korzystając z następujące eksperymentu myślowego. Otóż powiedzmy, że w pociągu jadącym z określoną prędkością, pewien obserwator zapala lampkę. Pociąg ten poruszający się będziemy traktowali jako układ O'. Obserwatora ten będzie obserwował bieg promieni światła wychodzących z lampki i powie, że światło to równocześnie dociera do każdej ściany wagonu w którym się znajduje. Jednak innego zdania będzie obserwator stojący obok przejeżdżającego pociągu. Według niego gdy w pociągu zapali się lampka, to światło szybciej dotrze do tylniej ściany wagonu, ponieważ ta porusza się w stronę źródła światła, natomiast więcej czasu zabierze dotarcie do przedniej ściany, ponieważ ta porusza się zgodnie z kierunkiem jego rozchodzenia się światła. Na tym prostym przykładzie widać, iż zdarzenie obserwowane jako jednoczesne w jednym układzie wcale nie musi być jednoczesne w drugim układzie. Fakt ten wynika bezpośrednio z transformacji Lorentza, według której czas nie płynie tak samo w układach poruszających się z różną prędkością. W tym wypadku określa się tak zwany interwał czasoprzestrzenny, czyli odległość pomiędzy dwoma zdarzeniami w czasoprzestrzeni.

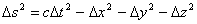
Dodatkowo według Einsteina interwał czasoprzestrzenny jest istotną wielkością, dla każdego zjawiska fizycznego, oraz jest on niezmienniczy względem transformacji. Niezmienniczość ta jest kolejnym bardzo ważnym postulatem Szczególnej Teorii Względności. Widać, że przy transformacji Galileusza, wszystkie pojedyncze zmienne czasoprzestrzenne były niezmiennicze. W transformacji Lorentza dopiero ich kombinacja, spełnia ten warunek.

7. Kinematyka w Szczególnej Teorii Względności

Otóż najważniejszymi wnioskami płynącymi ze Szczególnej Teorii Względności i transformacji Lorentza, jest skrócenie długości i dylatacja czasu. Dylatację czasu, czyli zwolnienie tempa upływu czasu w układzie poruszającym się z określoną prędkością, można wytłumaczyć korzystając tylko z pojęcia interwału czasoprzestrzennego. A mianowicie mamy dwa układy, jeden poruszający się z pewną prędkością - O', a drugi spoczywający względem niego - O. Obserwator znajdujący się w układzie O' zaobserwuje zjawisko, które odbywa się w miejscu, które on określi przy pomocy współrzędnej x'. Natomiast obserwator znajdujący się w układzie O, obliczy odległość czasoprzestrzenną, jako

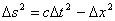
Pozostałych współrzędne znikają ponieważ nie ulegają one zmianie. Jeśli dodatkowo zauważymy, iż układ O' porusza się względem układu O z prędkością:

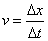
to otrzymamy ostatecznie wartość mierzonego czasu w układzie O:

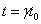
Czas t0 oznacza czas mierzony w układzie w którym dane zjawisko obserwuje się jako zjawisko będące w spoczynku. Zjawisko to określa się mianem relatywistycznego wydłużenia czasu, a w skrócie: dylatacją czasu.

Także długość ciała w układzie poruszającym się jest trochę inna niż w układzie spoczywającym. Do wytłumaczenia tego faktu posłużymy się transformacją Lorentza. Otóż dla obserwatora znajdującego się w układzie O', długość ciała wynosi

l' = x2' - x1'

Układ O', a więc także ciało to porusza się z prędkością v, względem obserwatora znajdującego się w układzie O. Na podstawie transformacji Lorentza pomiędzy układami O' i O, można obliczyć, że długość ciała mierzona w układzie O wynosić będzie:

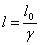
gdzie l0 oznacza długość ciała zmierzoną w układzie względem którego to ciało spoczywa, czyli w naszym przykładzie w układzie O'.

Jeżeli zastosuje się jeszcze transformację Lorentza do obliczenia reguły składania prędkości to otrzyma się wyrażenie:

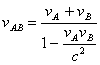
Widać, z niego, że żadne ciało nigdy nie może przekroczyć prędkości światła.

8. Dynamika w Szczególnej Teorii Względności

Skoro już wiemy, jak wyglądają prawa kinematyki dla ciał, które poruszają się z prędkościami bliskimi prędkościom światła, można się zastanowić jak wtedy będą wyglądać prawa dynamiki. Otóż według Einsteina to co nie powinno się zmienić, to obowiązywanie nadal zasad zachowania energii i pędu. Jednak wyrażenia na obliczenia pędu i energii ulegają pewnym modyfikacjom. Otóż wartość masy potrzebna do obliczenia wartości pędu czy energii, jest zależna od prędkości z jaką dane ciało się porusza zgodnie ze wzorem:

m = m0γ

gdzie m0 oznacza masę jako ma ciało w jego układzie spoczynkowym. Następnym postulatem jest równoważność pomiędzy masą i energią:

E = mc2

Natomiast wartość energii kinetycznej jest określana jako różnica pomiędzy energią jaką ciało ma będąc w ruchu, a energią spoczynkową tegoż ciała. Pojawia się także nowa wielkość określana nazwą czterowektora energii i pędu, którego wartość jest niezmiennicza względem transformacji Lorentza.

9. Siły bezwładności

Na ciało znajdujące się w układzie inercjalnym nie działają, żadne siły lub działające siły się równoważą. Natomiast w przypadku ciała znajdującego się w układzie nieinercjalnym, ciało to podlega działaniu pewnych sił. Siły te wynikają z istnienia pewnego przyśpieszenia z jakim układ nieinercjalny się porusza. Siły działające na to ciało bywają określane jako siły pozorne, ale częściej i bardziej adekwatnie jako siły bezwładności. Jeśli uwzględnimy takie siły przy opisie zachowania się ciała, to możemy stosować z powodzeniem zasady dynamiki Newtona. Otóż ciało znajdujące się w układzie nieinercjalnym On doznaje ono działania nie tylko sił, które są bezpośrednio do niego przyłożone, ale także siły, określanej mianem siły bezwładności, a wyrażającej się poprzez:

Fbezw = -man

Gdzie an jest wartością przyśpieszenia układu nieinercjalnego. Przykładem układu nieinercjalnego poruszającego się ruchem prostoliniowym, jest samochód, który przyspiesza, bądź zwalnia. Jednak ciekawszym przypadkiem jest układ nieinercjalny poruszający się po okręgu. Rozważmy taką sytuację, w której układ nieinercjalny obraca się z prędkością kątową ω. Układ ten ma ten sam początek układu współrzędnych jak układ inercjalny spoczywający. Rozważając taką sytuację, możemy obliczyć, jakie siły będą działać na ciało poruszające się z określoną prędkością v w tym układzie.

Fb=-2m*(ω x v)+m* ω x (W x r)

Element pierwszy tego wyrażenia nazywany jest siłą Coriolisa.

10. Bezwładność i grawitacja.

W zadach dynamiki Newtona mamy do czynienia z masą bezwładnościową ciała. Jednak istnieje także prawo powszechnego ciążenia korzystające z pojęcia masy ciała. Prawo to określa grawitację, czyli to w jaki sposób dwa ciała obdarzone masą oddziałują na siebie. Skoro zjawisko grawitacji i bezwładności to zupełnie dwa odrębne oddziaływania nasuwa się pytanie, czy masa bezwładnościowa, to jest to samo co masa grawitacyjna. Pytanie to zadało sobie także wielu fizyków, którzy przeprowadzili wiele doświadczeń mających na celu wykrycie różnicy pomiędzy tymi dwoma rodzajami mas. Z prawa powszechnego ciążenia wiadomo, że ciało jest przyciągane w kierunku Ziemi z siłą:

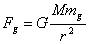
Siła ta z kolei na podstawie II zasady dynamiki Newtona jest równa:

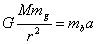
Czyli przyśpieszenie ciała zależałoby od wzajemnego stosunku masy grawitacyjnej i masy bezwładnościowej. Jednak w przeprowadzonych doświadczeniach wykazano, że masy te są równoważne sobie.

11. Równoważność masy grawitacyjnej i bezwładnościowej - konsekwencje.

Eksperymenty przeprowadzone wykazały, iż masa grawitacyjna i masa bezwładnościowa to te same wielkości. Stwierdzenie tej równoważności pomogło Einsteinowi przy opracowywaniu jego Ogólnej Teorii Względności. Einstein zauważył przy tym, że jeśli człowiek będzie zamknięty w jakimś pomieszczeniu, to w żaden sposób nie będzie mógł stwierdzić, czy odczucie ciężaru ciała jest wynikiem tego że znajduje się w układzie nieinercjalnym, czy też jest to wynik działania grawitacji. Można by było to stwierdzić jedynie w przypadku uwzględnienia większych odległości. Pozwoliłoby to na stwierdzenie w jaki sposób położenie w przestrzeni wpływa na wartość sił, a to z kolei by wskazało, czy mamy do czynienia z bezwładnością czy też z grawitacją. W przypadku np. spadającej windy w polu ciężkości Ziemi, wszystkie ciała znajdujące się w jej wnętrzu są w stanie nieważkości. Nieważkość ta wynika z równoważenia się siły przyciągania ziemskiego i siły bezwładności działającej na ciała we wnętrzu. Czyli daje to w sumie stwierdzenie, że na ciała znajdujące się w takiej windzie działające siły się równoważą, co jest treścią pierwszej zasady dynamiki, definiującej pojęcie układu inercjalnego. Grawitacja powoduje zakrzywienie czasoprzestrzeni wokół niej, potwierdzeniem tego faktu są obserwacje dotyczące przejścia światła w pobliżu obiektów o bardzo dużej masie.

12. Odwracalność i nieodwracalność procesów.

Określenie procesu odwracalnego używa się dla zjawiska, które jest niezmiennicze względem odwrócenia w czasie. Przykładami takich procesów są procesy zachodząc w świecie mikroskopowym: oddziaływania między atomami, lub cząsteczkami. Procesy natomiast nieodwracalne, w pewien sposób wyznaczają kierunek upływu czasu. Ich istotą jest to, że w czasie swojej ewolucji w czasie przechodzą do układów o wyższym stopniu nieuporządkowania.

13. Entropia

Wartość takiego nieuporządkowania określa parametr termodynamiczny: entropia. Mówi nam on o tym, na ile sposobów dany układ makroskopowy może zostać zrealizowany przez stany mikroskopowe. Entropię określa się poprzez wyrażenie:

S = -kB lnW

Gdzie kB oznacza stałą Boltzmana, a W ilość możliwych stanów mikroskopowych, jakie mogą zrealizować dany stan makroskopowy układu. W przypadku układu odizolowanego, wszystkie procesy zachodzące prowadzą do osiągnięcia przez układ równowagi termodynamicznej, czyli maksymalnej wartości entropii.

14. Zasada ekwipartycji

Równanie stanu gazu doskonałego:

pV = nRT

gdzie p - ciśnienie gazu, T - temperatura gazu, V - objętość gazu, n - liczba moli gazu, R - uniwersalna stała gazowa.

Równanie to powstało wraz z powstaniem kinetyczno - mechanicznej teorii gazów. W teorii tej, gaz to zbiór cząsteczek, które poruszają się i zderzają ze sobą w sposób całkowicie przypadkowy. Mogą także zderzać się ze ściankami naczynia w którym się znajdują z równoczesnym przekazem pędu. Taki jest właśnie mechanizm powstania ciśnienia. Ciśnienie to wyraża się poprzez

 

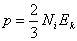
Jednak każda cząsteczka gazu, posiada inną energie kinetyczną, więc aby obliczyć adekwatną wartość ciśnienia należy się posłużyć średnią wartością energii poruszających się cząsteczek:

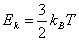
Energia ta nam mówi o tym, że jeśli chcemy zmienić temperaturę układu zawierającego 1 mol gazu, o powiedzmy 1 stopień to musimy dostarczyć do niego energii w ilości 3/2kNA=3/2R, a ponieważ (C­v=3/2R), energię taką określa się mianem ciepła molowego dla stałej objętości. Są to podstawy działania zasady ekwipartycji energii. Cząsteczki możemy traktować jako punkty, tylko w przypadku cząsteczek składających się z pojedynczych atomów. Taka cząsteczka może mieć trzy stopnie swobody, związane z położeniem jej w trójwymiarowym układzie współrzędnych. Zasada ekwipartycji energii mówi nam, że dla każdego stopnia swobody, rozumianego w sposób klasyczny przypada energia równa kBT/2, co w sumie dla 3 stopni swobody daje 3kBT/2. A co to znaczy, że dany stopień jest rozumiany w sposób klasyczny. Tylko tyle, że odpowiadający mu ruch, można opisać za pomocą praw mechaniki klasycznej.

15. Tłumione drgania swobodne

Jeżeli siła działająca na ciało jest proporcjonalna do jego wychylenia, to mówimy, że siła ta ma charakter sprężysty i spełnia ona prawo Hooke'a:

F = -kr

Pod wpływem działania takiej siły sprężystości, ciało porusza się ruchem harmonicznym, który opisuje równanie

x(t) = x0cos(ωt+φ)

Jest to tzw. rozwiązanie równania oscylatora harmonicznego nie tłumionego.

Jednak w przypadku rzeczywistym, zawsze mamy do czynienia z siłami tarcia, które w przypadku ruchu ciała są proporcjonalne do jego prędkości:

T = -fv

Daje to nam wraz z siłą sprężystości, siłę wypadkową działająca na oscylator harmoniczny. Korzystając następnie z II zasady dynamiki Newtona możemy otrzymać równanie ruchu dla takiego oscylatora:

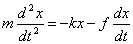
Rozwiązująć to równanie otrzymujemy wyrażenie na zależność położenia ciała oscylującego od czasu:

 

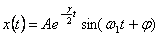
Widać, że amplituda ruchu harmonicznego maleje w sposób eksponencjalny z czasem, i to tym szybciej im większą ma wartość parametr tłumienia γ. Przy jego dostatecznie dużej wartości, ciało w ogóle nie wykonuje ruchu harmonicznego, a jedynie powoli wraca do położenia równowagi. W przypadku drgań tłumionych definiuje się tzw. czas życia, czas relaksacji, określający czas po którym amplituda w ruchu harmonicznym zmaleje e razy:

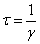
Definiuje się dodatkowo także tzw. współczynnik dobroci Q mówiący o tym, jaka cześć energii oscylatora zostaje utracona w przeciągu 1 okresu.

16. Oscylator harmoniczny tłumiony z siłą wymuszającą

Aby w oscylatorze harmonicznym tłumionym podtrzymywać nadal drgania, należy wprowadzić pewną siłą, która by podtrzymywała te drgania. Siła ta musi mieć charakter harmoniczny, czyli musi działać z określoną częstością:

F = F0sin(wt)

To prowadzi do równania ruchu postaci:

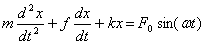
Jest to równanie różniczkowe niejednorodne, którego rozwiązaniem jest funkcja:

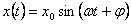
gdzie:

Jak widać wielkości wychylenia - amplituda oscylatora, silnie zależy od częstotliwości siły wymuszającej - ω. Możliwe jest takie dopasowanie tejże częstotliwości, aby drgania miały maksymalną amplitudę. Wartość takiej częstotliwości określana jest mianem częstotliwości rezonansowej i wyraża się poprzez:

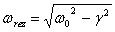
Zjawisko rezonansu polega na tym, iż oscylator przy odpowiedniej częstotliwości siły wymuszającej, pobiera całą energię jakiej dostarcza siła do układu.

17. Rezonatory

Rezonatorami nazywamy urządzenia, które wykorzystują zjawisko rezonansu do generacji drgań, są kluczowymi elementami każdego urządzenia które generuje drgania harmoniczne, także instrumenty muzyczne.

18. Fale

Fala jest to zaburzenie rozchodzące się w określonym ośrodku. Fale można rozumieć jako zbiór oscylatorów harmonicznych połączonych ze sobą i drgających we wzajemnej korelacji. Każda fala porusza się w danym ośrodku z określoną prędkością.

19. Energia fali.

Fala mimo tego, że nie transportuje masy w czasie swej propagacji, transportuje energię. Rozpatrzmy falę, która porusza się z prędkością v w kierunku dodatnich wartości osi x. Jako, że falę można rozumieć jako zbiór oscylatorów, to każdy taki oscylator ma określoną energię. Teraz jeśli fala ta przechodzi przez wycinek powierzchni dS, w czasie równym dt, i w tym czasie przetransportowała ilość energii równą DE, to można określić natężenie takiej fali I. Oznaczając gęstość energii poprzez Er, otrzymamy wyrażenie na natężenie fali:

I = Erv

To po kolejnych obliczeniach finalnie da nam wartość:

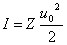
gdzie: Z - jest to wartość określająca falową oporność ośrodka,

u0 - jest to amplituda prędkości drgań.

Dla fal charakteryzuje się także moc M jaką fala posiada, czyli jak szybko fala dostarcza określoną ilość energii w jednostce czasu. Korzystając z pojęcia mocy, można wyrazić natężenie fali jako stosunek mocy do powierzchni przez jaką fala przechodzi:

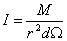
Wielkość dΩ określa kąt bryłowy określający tą powierzchnię. W przypadku przejścia fali przez określony ośrodek, następuje jej stopniowe wygaszenie. Zmiana natężenie wtedy fali wynosi

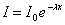
gdzie parametr λ określa tzw. współczynnik pochłaniania fali.

20. Interferencja fal.

W przypadku kilku źródeł fal, które nakładają się na siebie, występuje zjawisko określone jako superpozycja fal. Drgania składowe każdej z fal dodają się do siebie tworząc drganie wypadkowe - wypadkową fale. W przypadku dwóch fal o podobnych częstotliwościach i podobnych wektorach falowych, ale identycznych amplitudach:

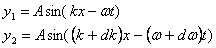
Dostajemy drganie wypadkowe powstałe z ich złożenia określone równaniem:

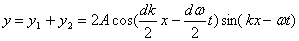
Widzimy więc, że fala wypadkowa, posiada tez sam wektor falowy i częstotliwość jak fale składowe, tylko amplituda się zmienia z określoną częstotliwością, jest modulowana. Co ciekawe to jeśli wykreślimy wokół amplitudy jej obwiednie, spostrzeżemy, iż obwiednia ta ma kształt fali, poruszającej się z prędkością:

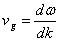
która jest określana mianem prędkości grupowej. Prędkość grupowa, określa niejako szybkość transportu energii, jakiego fala dokonuje.

Istnieje także inny rodzaj prędkości, która charakteryzuje poruszającą się falę, jest to prędkość fazowa:

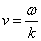
W przypadku gdy rozchodzenie się fali w danym ośrodku, gdy prędkość fazowa tej fali w tym ośrodku, zależy od jej długości fali, to taki ośrodek nazywamy ośrodkiem dyspersyjnym.

21. Paczka falowa.

W przypadku rzeczywistym, każda fala gdzieś się kończy i gdzieś się zaczyna. Czyli rzeczywista fala nie jest funkcją harmoniczną, ponieważ ta rozciąga się, aż do nieskończoności. Na określenie fali, która jest ograniczona w czasoprzestrzeni, używa się terminu paczki falowej. Każda taka paczka falowa ma prędkość grupową równą prędkości grupowej fali, która ją tworzy. Każda fala, która jest postaci paczki falowej, jest falą złożoną, czyli powstała w wyniku złożenia kilku drgań harmonicznych.

22. Interferencja fal pochodzących ze źródeł punktowych

Mając do dyspozycji siatkę z widocznymi na niej n - punktami, przepuszczając przez nią falę, można zaobserwować zjawisko interferencji. Jeśli punkty te znajdują się w we wzajemnej odległości d, to warunkiem na powstanie maksimów interferencyjnych jest to aby:

dsin(φ)=nλ

gdzie λ jest długością fali padającej. Czyli w skrócie mówiąc różnica dróg optycznych pomiędzy dwoma falami których źródłami są punkty na siatce, powinna być wielokrotnością długości fali padającej.

23. Zasada Huyghensa.

Zasada Huyghensa mówi o tym, że każdy punkt do którego dojdzie fala, staje się źródłem nowej fali. Jeśli takich punktów jest wiele, to w wyniku nałożenia się nowo powstałych fal, może powstać charakterystyczny front falowy. W przypadku, gdy fala natrafi na pewien otwór, to staje się on źródłem nowej płaskiej fali. Jeśli otwór ten nie jest punktowy, to następuje ugięcie fali na otworze, zjawisko to nazywa się dyfrakcją fali. Jednak ugięcie fali nie następuje tylko w wyniku padania fali na okrągłe przedmioty. Także w przypadku innych kształtów, obserwowane jest zjawisko dyfrakcji. To jaki będzie kształt nowej ugiętej fali, bezpośrednio zależy od kształtu fali padającej, oraz od kształtu przeszkody, która spowodowała ugięcie. Zasada Huyghensa, okazała się bardzo ważnym narzędziem przy konstruowaniu zasad rządzących optyką geometryczną. To dzięki niej powstały zasady odbicia i załamania fal na granicach ośrodków.

24. Dyfrakcja fali na obiektach rzeczywistych.

Jak już wiemy dyfrakcja fali, jest to ugięcie się fali na określonej przeszkodzie. W wyniku tego fala zmienia swój kierunek rozchodzenia się. Wyjaśnienie kształtu i sposobu propagacji fali, która natrafiła na kołowy otwór o średnicy D, można przeprowadzić zakładając że otwór ten jest skrajnym przypadkiem siatki interferencyjnej, w ten sposób, że (N-1)*d=D. Przeprowadzając analizę w ten sposób, można znaleźć warunki wygaszenia i wzmocnienia fali. Otóż dla kąta φ=0 nastąpi maksymalne wzmocnienie fali, natomiast wygaszenie dla kąta dφ = l/D, a także dla kolejnych wielokrotności kąta dφ.

25. Holografia.

Metoda holografii, pozwala nam na ujrzenie głębi rejestrowanych obrazów. Normalnie każde zdjęcie jest płaskie, ponieważ rejestruje tylko natężenie fali padającej, czyli światła. Jednak informację o głębi obrazu niesie ze sobą przesunięcie fazowe fali. Oko ludzkie, jest w wstanie rejestrować to przesunięcie. W metodach holograficznych, wykorzystuje się zjawisko interferencji. Otóż pierwszym etapem jest rejestracja obrazu na kliszy, za pomocą fali ugiętej na przedmiocie który podlega rejestracji. Jednak, aby uzyskać także informacje o zmianie fazy fali ugiętej na przedmiocie, kliszę fotograficzną oświetla się także wiązką odniesienia. W ten sposób na kliszy powstaje obraz interferencyjny, powstały w wyniku nałożenia się fali ugiętej i fali odniesienia. Co z kolei daje nam informacje o przesunięciu fazowym.

26. Charaketerystyki kierunkowe odbiorników i nadajników.

W przypadku emitowania fal, ważnym jest to aby mogły się rozprzestrzeniać we wszystkich możliwych kierunkach. Idealnym tutaj zastosowaniem, jest użycie punktu emitującego fale, dzięki czemu fale te mogłyby się propagować w każdą stronę. Jednak, jakie źródło należy zastosować w przypadku, gdy chcemy emitować fale w jednym określonym kierunku. Najlepszym rozwiązaniem w ukierunkowaniu fali jest zastosowanie zwierciadła o kształcie paraboidalnym. Jeśli w jego ognisku umieścimy źródło fali, to emisja będzie się odbywać tylko w kierunku równoległym do kierunku osi zwierciadła. Zastosowania zwierciadła o takim kształcie powoduje skupienie fal wychodzących ze źródła tworząc w ten sposób wiązkę o kształcie koła, równego rozmiarom tego zwierciadła. W przypadku odbiorników punktowych, ich czułość nie jest zawsze izotropowa. Jednak przy zastosowaniu wielu takich odbiorników i złożeniu ich w postać siatki inerferencyjnej, można sumować odbierane sygnały z uwzględnieniem przesunięcia fazowego. Taki układ odbiorników będzie miał taką samą charakterystykę kierunkową jak układ nadawczy. Gdy odbiornik i nadajnik mają takie same kształty geometryczne, ich charakterystyki kierunkowe, także są identyczne. Zagadnieni ściśle określonej charakterystyki kierunkowej znajduje zastosowanie w przypadku badań kosmosu za pomocą radioteleskopów. Takie radioteleskopy wyposażone są w olbrzymie anteny, które muszą być tak ustawione, aby odbierać tylko sygnał z określonego źródła we Wszechświecie. Czyli pojawia się tutaj zagadnienie uzyskania jak najlepszej rozdzielczości kątowej anteny, tak aby móc w stanie rozróżnić bardzo odległe od siebie źródła fal. Po to właśnie radioteleskopy buduje się tak wielkich rozmiarów, gdzie często średnica anteny przekracza 100 metrów. Aby uzyskać jeszcze lepszą zdolność rozdzielczą, synchronizuje się ze sobą wiele radioteleskopów odległych od siebie o tysiące kilometrów. Powoduje to polepszenie charakterystyki kierunkowej całego układu, ponieważ wtedy jest to iloczyn odległości pomiędzy elementami układu, oraz charakterystyki kierunkowej danego elementu układu. To zdecydowanie polepsza zdolność rozdzielczą takiego układu anten.

27. Zachowanie się fali na granicy ośrodków.

Padająca fala na pewien ośrodek, powoduje że część jej ulega odbiciu, a część wnika do ośrodka. Przy przejściu fali do drugiego ośrodka, następuje zjawisko załamania fali, które jest opisywane prawem załamania:

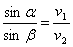
Jak wynika z zasady zachowania energii, suma natężeń fali odbitej i fali załamanej musi zgadzać się z natężeniem fali padającej: IO + IZ = I. IO - natężenie fali odbitej, IZ - natężenie fali załamanej, I - natężenie fali padającej. Na granicy ośrodków muszą być spełnione tzw. warunki ciągłości. W tym miejscu amplitud, prędkość i ciśnienie fali padającej oraz fali odbitej, muszą wynosić tyle samo co dal fali załamanej.

Dla amplitud: Y + YO = YZ

Dla prędkości: u + uO = uZ

Dla ciśnień: p + pO = pZ

Dodatkowo wprowadza się parametry charakteryzujące oba ośrodki graniczące ze sobą. Tymi parametrami są tzw. oporności falowe ośrodków Z1, Z2.

Z powyższych zależności można wyznaczyć tzw. współczynnik odbicia R opisujący jaka część fali została odbita. Współczynnik ten wynosi:

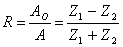
Korzystając z tego współczynnika można wyliczyć, jakie jest natężenie fali odbitej, a jakie fali załamanej.

IO = R2I

IZ = (1-R2)I

Na podstawie tych natężeń, widać, że to jaka część fali zostanie odbita, a jaka załamana, zależy tylko od właściwości ośrodków, na granicy których dochodzi do odbicia i załamania. Można łatwo zauważyć, że w przypadku, gdy Z1 = Z2, to R = 0 i mamy ośrodek ciągły, fala przechodzi w całości, nie ma żadnego odbicia. Odbicie następuje wtedy gdy R jest różne od 0.

28. Fale stojące.

Może się zdarzyć, że przy prostopadłym padaniu fali na granicę dwóch ośrodków, fala odbita będzie miała ten sam kierunek, co fala padająca, ale przeciwny zwrot. Dojdzie wtedy do interferencji, co z kolei może prowadzić do powstania fali stojącej. Równanie opisujące taką fale stojącą:

Ys= Y + Yo =2Acos(kx)sin(ωt)

Jak widać równanie to nie przypomina równania opisującego równanie fali, ponieważ argument funkcji sinus nie zależy od wektora falowego k. Równanie to raczej opisuje drganie stacjonarne w czasie, z amplitudą zależną od położenia. Teraz w przypadku gdy ośrodek w którym znajduje się fala padająca ma większą oporność falową od ośrodka na który fala pada, to przy granicy ośrodków powstanie tzw. strzałka. W przypadku odwrotnym na granicy powstanie tzw. węzeł. Z kolei jeśli ośrodek w którym znajduje się fala padająca, jest ograniczony z dwóch stron przez ośrodek, na który fala pada i w przypadku gdy ośrodek ten zapewnia całkowite odbicie fali, to fala stojąca jest ograniczona z obu stron. Układ tak zbudowany jest określany mianem rezonatora. Rezonator może mieć tylko ściśle określoną długość fali, a mianowicie musi być ona wielokrotnością połowy długości fali odbijanej - λ. To prowadzi także do tego, że rezonator może drgać tylko ze ściśle określonymi częstotliwościami. W rzeczywistości najczęściej spotyka się rezonatory trójwymiarowe, które ograniczają w swoim wnętrzu, także fale rozchodzące się w przestrzeni trójwymiarowej.

29. Pole elektryczne - indukcja, natężenie, potencjał.

Ładunek q znajdujący się w polu elektrycznym podlega działaniu siły F. Cechę tą opisuje wielkość zwana natężeniem pola elektrycznego E i równa E = F/q. Oprócz natężenia pola elektrycznego inną wielkością która może opisywać pole, jest potencjał elektryczny. Jest on określany dla danego punktu pola, jako praca jaką należy wykonać, aby przenieść ładunek q z punktu B do punktu A:

VA - VB = WAB/q

Jednak najczęściej przyjmuje się, że punkt B leży w nieskończenie dużej odległości, tak dużej że potencjał dla tego punktu wynosi 0. I zwyczajowo podaje się że potencjał pola elektrycznego w danym punkcie A, to praca jaką należy wykonać, aby przenieść ładunek q z nieskończoności do punktu A. I wtedy potencjał jest określany jako: V = W/q.

Jeżeli teraz wyrazimy pracę WAB jako:

WAB = Fdl

I po podstawieniu F =qE, otrzymamy:

VA = Edl

Jest to związek pomiędzy potencjałem elektrycznym, a natężeniem pola elektrycznego w danym punkcie. Jak widać wielkości te są silnie uzależnione od siebie.

Pole elektryczne, może także powstać w wyniku indukcji elektrostatycznej. Indukcja elektrostatyczna jest zjawiskiem polegającym na rozdzielaniu różnoimiennego ładunku. Pole które zostało wyindukowane, określa wektor indukcji pola elektrycznego D. Wartość tego wektora ściśle zależy od wielkości wyindukowanego ładunku. Pomimo tego, że wektor D, został osobno zdefiniowany, bez użycia wektora natężenia pola elektrycznego E, to w wyniku przeprowadzonych doświadczeń okazało się, że istnieje pomiędzy nimi związek:

D = ε0E

30. Prawo Gaussa

Jeśli zamkniemy ładunek Q we wnętrzu ograniczonej powierzchni, która jest przewodnikiem, to spowoduje to wyidukowanie ładunku na zewnątrz tej powierzchni. Wielkość wyindukowanego ładunku, będzie wynosić Q. Dzięki temu prawu, bardzo łatwo możemy obliczyć, jakie pole wytwarza dany ładunek, pod warunkiem, że rozkład tego ładunku, jest w pewnym sensie symetryczny. Dla przykładu weźmy ładunek punktowy, o wartości Q. Ładunek taki wytwarza pole wokół niego o symetrii sferycznej. Jeśli teraz zastosujemy prawo Gaussa w sposób taki, że ładunek ten ograniczymy kulistą powierzchnią o środku w punkcie gdzie się znajduje ładunek i promieniu r, to wektor indukcji D jest w każdym punkcie prostopadły do tej powierzchni. To z kolei zaprowadzi nas do obliczenia prostej całki, której wynik da nam wartość pola elektrycznego:

E = Q/(4πε0r2)

Jeśli teraz podstawimy to pole do związku F = qE, otrzymamy znane prawo Culomba, opisujące oddziaływanie na siebie ładunków elektrycznych.

F = (qQ)/(4πε0r2)

31. Elektryczny dipol.

Dipol elektryczny to układ złożony z dwóch ładunków o przeciwnych znakach, znajdujących się względem siebie w odległości l. Parametrem charakterystycznym, określającym dipol jest jego tzw., moment dipolowy, czyli:

p = ql

Jeśli taki dipol umieścimy w obszarze pola elektrycznego, to zauważymy działanie na niego momentu siły:

M = F l sinφ = E p sinφ

Powyższą zależność można zebrać do postaci iloczynu wektorowego:

M = p x E

W ten sposób możemy wywnioskować, iż pole elektryczne działa na dipol w ten sposób, że próbuje ustawić go, wzdłuż kierunku pola. Oczywiście takiemu działaniu musi towarzyszyć wykonanie pracy przez pole elektryczne. Skoro praca ta się pojawia, musi ona wprowadzić zmianę energii potencjalnej dipola. Dzięki temu możemy obliczyć ile wynosi energii potencjalna dipola znajdującego się w polu elektrycznym:

U = -p E

Gdy mamy do czynienia z dipolem znajdującym się w polu elektrycznym jednorodnym, to siła wypadkowa działająca na ten dipol jest równa 0. Jednak w przypadku niejednorodnego pola, siła wypadkowa, jest niezerowa, co powoduje ustawienie się dipola w kierunku linii sił pola. Jako że dipol jest układem dwóch ładunków, on także wytwarza wokół siebie pole elektryczne, pole to obserwowane na dużych odległościach od dipola wynosi:

E = p/(4πε0r3)

32. Pole magnetyczne - natężenie i indukcja.

Pole magnetyczne jest polem, które przekazuje oddziaływania magnetyczne. Tym oddziaływaniom nie podlegają statyczne ładunki elektryczne, ponieważ nie tworzą one wokół siebie pola magnetycznego. Warunkiem tego, aby powstało pole magnetyczne, jest ruch ładunku elektrycznego. Inaczej mówiąc aby ładunek elektryczny poczuł działanie na niego pola magnetycznego musi się poruszać. Do opisu pola magnetycznego używa się dwóch wielkości charakterystycznych: natężenia pola magnetycznego H i indukcji pola magnetycznego B. Wektor indukcji magnetycznej jest wielkością charakteryzującą dynamiczność danego pola. Jest on określany poprzez zależność wiążącą siłę F, jaka działa na przewodnik o długości l, znajdujący się w polu o indukcji magnetycznej B i w którym płynie prąd o natężeniu I:

F = l I x B

Siła ta wynika z tego, iż każdy elektron poruszający się z prędkością v, znajduje się w obszarze pola magnetycznego B i doznaje działania siły Lorentza FL:

FL = q v x B

Drugim parametrem określającym własności pola, jest wektor natężenia pola magnetycznego. Związek pomiędzy wektorem H, a wektorem B, określają równania Maxwella. Tak samo jak w przypadku pola elektrycznego, także tutaj możemy wprowadzić pojęcie linii sił pola. Jednak w tym przypadku linie te są zamknięte, a o ich kierunki i zwrocie decyduje reguła śruby prawoskrętnej.

33. Prawo Ampera.

Prawo Ampera określa zależność pomiędzy wartością prądu płynącego w przewodniku, a wielkością natężenia pola magnetycznego, jakie powstało w wyniku tego przepływu. Korzystając z tego prawa, otaczamy przewodnik w którym płynie prąd I, konturem o długości l. Teraz oznaczamy składową styczną H­l do konturu. Otóż prąd jaki płynie w przewodniku wynosi:

I = Hldl

Teraz wystarczy tylko przeprowadzić całkowanie po całej długości konturu. Wynik da nam wartość natężenia pola wokół przewodnika:

H = I/(2πR)

Pomiędzy wektorem natężenia pola magnetycznego H a wektorem indukcji magnetycznej B istnieje związek

H= μ0 B

Pole magnetyczne dla solenoidu można w podobny sposób obliczyć, korzystając z prawa Ampera, jak w przypadku prostego przewodnika. Ponieważ pole to istnieje tylko wewnątrz solenoidu, oraz jest ono w tym obszarze to wynosi:

H = I N/l

Gdzie N oznacza liczbę zwojów, a l długość solenoidu.

34. Cząstka o określonym ładunku poruszająca się w polu magnetycznym.

Na cząstkę obdarzoną ładunkiem q i poruszająca się z prędkością v w obszarze pola magnetycznego B, działać będzie siła Lorentza:

F = q v x B

Jako że siła ta jest wynikiem iloczynu wektorowego, widać że kierunek jej działania będzie bezpośrednio zależał od wzajemnej orientacji wektorów prędkości i indukcji magnetycznej. Jeśli kierunek prędkości cząstki jest równoległy do kierunku wektora indukcji magnetycznej to cząstka ta nie będzie odczuwać działania siły Lorentza. Dla przypadku gdy kierunek prędkości będzie prostopadły do kierunku wektora B, siła ta będzie siłą dośrodkową zakrzywiająca tor lotu cząstki, ale nie zmieniającą jej prędkości. Cząstka wtedy będzie się poruszać po okręgu o promieniu:

R = (Ul v)/(q B)

35. Dipol magnetyczny.

Przykładem dipola magnetycznego może być pętla przewodnika, w którym płynie prąd o natężeniu I. Tak jak w przypadku dipola elektrycznego także tutaj możemy określić wielkość zwaną momentem dipolowym magnetycznym. Moment ten wynosi:

P = S I n

Dipol magnetyczny znajdujący się w polu magnetycznym doznaje działania siły o momencie:

M = p x B

Także możemy określić energię potencjalną jaką ma dipol magnetyczny:

U = - p B

Elementarnym dipolem magnetycznym jest ładunek q krążący po kołowej orbicie. Natężenie prądu wtedy wynosi I = q n, gdzie n określa częstotliwość obrotów. Wtedy moment magnetyczny takiego dipola wynosi:

P = qK/2m

Gdzie K oznacza kręt elektronu, jego moment pędu. Kręt jest skwantowany, tak więc i moment dipolowy magnetyczny, także będzie wielkością skwantowaną. Oprócz zwykłego krętu cząstka posiada także własny moment pędu, czyli spin. Spin jest także skwantowany. Określa się jednostkę momentu magnetycznego, użyteczną przy określaniu własności atomów i molekuł - tzw. magneton Bohra: mB=(e/2m)*h/2π

36. Prawa indukcji Faradaya. Równania Maxwella.

Gdy mamy strumień indukcji magnetycznej przepływający przez zamkniętą powierzchnię która jest ograniczona przewodnikiem, to gdy ten strumień ulegnie zmianie w przewodniku okalającym go popłynie prąd. Innymi słowy: zmiana strumienia induksji magnetycznej ΦB, powoduje powstanie siły elektromotorycznej:

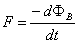
Zasadniczą częścią tego twierdzenie, jest fakt że zawsze gdy indukcja magnetyczna ulega zmianie, powoduje to wyindukowanie wirowego pola elektrycznego. Prawo to jest treścią jednego z równań Maxwella:

 

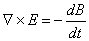
37. Zastosowanie indukcji elektromagnetycznej.

Gdy nie prawo Faradaya, dzisiaj nie istniałaby elektryczność. Dzięki temu, że poprzez zmianę strumienia indukcji magnetycznej, można wytworzyć pole elektryczne, możliwym się stało wytwarzanie prądów zmiennych w czasie. Zjawisko to w szczególności stanowi podstawę działania transformatora. Wielkością charakteryzującą strumień indukcji magnetycznej powstały w obszarze ograniczonym obwodem, jest tzw. indukcyjność L. Indukcyjność ta bezpośrednio zależy od geometrii obwodu, i wielkości charakteryzującej dany materiał - od przenikalności magnetycznej. W przypadku solenoidu indukcyjność wynosi:

L = μ μ0 S z2/l

Gdzie wielkości S, z i l charakteryzują geometrię przewodu, S - jest przekrojem poprzecznym obwodu, z - ilością zwojów, a l długością całego solenoidu. W przypadku prądu zmiennego, siła elektromotoryczna wynosi:

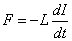
Tak więc należy zrównoważyć tą powstałą siłę elektromotoryczną poprzez zastosowanie zewnętrznego określonego źródła prądu.

Jako że każdy przewód, charakteryzują wielkości takie jak opór R, czy indukcyjność L, prąd powstały nie od razy zacznie płynąć z określonym natężeniem. To jak szybko wzrośnie jego wartość od 0 do określonej wartości dla danego układu, zależy od stosunku L/R. Zależność ta ma przebieg wykładniczy. W przypadku, gdy powstałe w wyniku przepływu prądu pole magnetyczne, obejmuje obszar w którym znajduje się inny przewodnik w którym także płynie prąd, to pojawia się zjawisko sprzężenia strumienia indukcji. W tym wypadku określa się indukcję tzw. wzajemną L. Jest to wielkość bardzo ważna, a w przypadku transformatorów im jest ona większa tym większa moc transformatora.

38. Równania Maxwella.

Jest to zbiór równań określających związki pomiędzy polami elektrycznymi a magnetycznymi. Dzięki nim dokonała się ostateczna unifikacja teorii pól elektrycznych i teorii pól magnetycznych w jedną spójną teorię magnetyzmu. Jest to zbiór 4 równań, które w postaci różniczkowej prezentują się następująco:

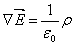 - jest to treść prawa Gaussa.

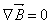 - prawo to nie ma sprecyzowanej nazwy, a mówi nam o tym, że w przyrodzie nie obserwujemy czegoś takiego jak ładunki magnetyczne.

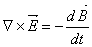 - jest to treść prawa Faradaya

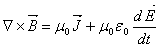 - jest to poprawione przez Maxwella prawo Ampere'a

39. Promieniujący dipol elektryczny

Jak już wiemy statyczne ładunki elektryczne wytwarzają tylko pole elektryczne. Ładunki, które się poruszają dodatkowo wytwarzają także pole magnetyczne. Natomiast w przypadku ładunku poruszającego się ruchem zmiennym wytwarzają promieniowanie elektromagnetyczne - falę elektromagnetyczną. Można to bezpośrednio wykazać opierając się na równaniach Maxwella. Fala taka powstaje w przypadku, gdy ładunek porusza się z określonym przyśpieszeniem. Jeśli rozwiążemy dla tego zagadnienia równania Maxwella, to otrzymamy. Ważna jest zależność czasowa tak powstałego pola, a mianowicie, że natężenie pola w chwili t, zależy od tego w jakim stanie był ładunek w momencie wysłania tej fali elektromagnetycznej. Bardzo ważnym przypadkiem emitowania fali elektromagnetycznej jest promieniowanie drgającego dipola elektrycznego. Otóż w przypadku drgającego z amplitudą l, ładunku Q, zostaje emitowane pole magnetyczne. Pole to jest takie samo, jak gdyby było emitowane przez dipol drgający o momencie p = Q l. Taki jest właśnie mechanizm promieniowania fal elektromagnetycznych przez atomy, molekuły cząsteczki. Dzięki temu zjawisku powstaje promieniowanie widzialne, rentgenowskie podczerwone, promieniowanie gamma. W ten sposób także działają anteny emitujące fale radiowe. Możemy obliczyć natężenie pola elektrycznego, jakie jest wtedy emitowane, a dokładniej jego amplitudę:

E0=(p*ω2*sinθ)/(4 π ε0 c2 r)

Dodatkowo możemy obliczyć moc takiego promieniowania. W tym celu dokonujemy całkowania natężenia fali przechodzącej przez powierzchnię kuli o promieniu r. Wynosi ona:

P = (p2 ω4)/(12π ε0 c3).

Jest to moc drgającego dipola o momencie elektrycznym p.

40. Obwód elektryczny emitujący falę elektromagnetyczną.

Otóż zakładamy, że w danym obwodzie płynie prąd elektryczny dokładnie określony przez siłę elektromotoryczną. Oraz że w każdej chwili w obwodzie prąd jest taki sam jak określony przez siłę elektromotoryczną. Jednak, jak wiemy każde ciało porusza się ze skończoną prędkością. Także pole elektryczne, które porusza się z prędkością światła. Jeśli mamy dane pole elektryczne w odległości l od źródła zasilania i rejestrujemy je w chwili t, to zostało ono wytworzone przez siłę elektryczną w chwili czasu t - l/c. Gdy mamy do czynienia z siłą elektromotoryczną SEM harmoniczną, to powstające pole elektryczne płynące w obwodzie ma postać fali. W przypadku gdy obwód nie jest zwarty na końcach, przez przewód także płynie prąd. Z kolei, jeśli długość fali pola, jest w korelacji z długością samego obwodu, to w tymże obwodzie może powstać fala stojąca, ponieważ fala po dojściu do rozwartego końca obwodu ulega odbiciu. Jeżeli źródło zasilające ma odpowiednio dopasowane natężenie o określonej częstotliwości, to w przewodniku może powstać fala stojąca prądu. Prowadzi to do tego, że taki obwód z taką falą stojącą zachowuje się jak drgający dipol, czyli może być źródłem fali elektromagnetycznej. W ten sposób można zbudować antenę nadawczą, która jest nazywana dipolem.

41. Antena dipolowa.

Tak jak wykazano wcześniej możliwe jest zbudowanie anteny nadawczej, która jest określana mianem dipola. Jest to bardzo typowy przykład anteny nadawczej. W antenach takich stosuje się tylko jedno ramie, w postaci wysokiego masztu. Antena taka jest osadzona w ziemi, która jest dla takiej anteny, dla takiego dipola powierzchnią o stałym potencjale. To z kolei powoduje, że linie powstałego pola, układają się w taki sposób jakby ziemia była zwierciadłem, które dopełnia brakującą część obwodu odbijając emitowany sygnał.

Oprócz dipola elektrycznego, promieniowanie elektromagnetyczne, może także emitować dipol magnetyczny, który drga.

42. Światło spójne i niespójne.

Światło powstaje w wyniku procesu przechodzenia atomów pomiędzy poziomami energetycznymi. Jest to najczęściej wynik przejścia atomu ze stanu wzbudzonego do stanu podstawowego. Przy takim przejściu atom wypromieniowuje nadwyżkę energii w postaci promieniowania elektromagnetycznego. Takie przejścia zachodzą przypadkowo i nie wpływają na siebie, dlatego też powstałe światło w wyniku takich przejść jest określane mianem światła niespójnego. W przypadku, gdy atomy znajdują się względem siebie w bliskim sąsiedztwie, istnieją wtedy pewne warunki pozwalające na zsynchronizowanie emisji, jednak im są one dalej położone od siebie, tym mniejsze jest prawdopodobieństwo na zaistnienie takiego efektu. Źródła światła, które mogłyby być źródłami światła spójnego, powinny osiągać rozmiary rzędu długości fali świetlnej, naturalne takie źródła przyjmują rozmiary ok. 1 μm. Jednak dla przypadku, gdy mamy źródło światła niespójnego o rozmiarze D, to światło docierające z niego do określonego punktu P, ma dokładnie określoną fazę. Wynika to z tego, że wszystkie fale składowe pochodzące od źródła nakładają się na siebie, a faza każdej z nich nie może się znacząco różnić od pozostałych. Jeśli dokona się pomiaru takiej różnicy faz, dla dwóch różnych punktów znajdujących się na oświetlonej powierzchni i wyrazi się ją jako różnice dróg fal, to otrzyma się:

dr = Dsindφ = Ddφ

I jeśli ta różnica dróg jest dużo mniejsza od 1, to znaczy, że różnica faz jest dużo mniejsza od 2π. To z kolei prowadzi do wniosku, że mimo iż światło nie jest spójne, to obszar który oświetla jest w przybliżeniu oświetlony spójnie.

Oczywiście istnieją światła spójne, jednym z takich przykładów jest laser, który obecnie jest wykorzystywany praktycznie w każdej gałęzi przemysłu. Oprócz tego, że jest to światło spójne to jeszcze jest chromatyczne. Ciekawą własnością lasera, jest jego duża moc przypadająca na element powierzchni. Dodatkowo jeżeli użyjemy soczewki do skupienia jego światła, to amplituda fali emitowanej wzrośnie aż 40 razy. Co za tym idzie natężenie czyli kwadrat amplitudy wzrośnie aż 1600 razy.

43. Interferencja światła niespójnego.

Jest to interferencja kilku wiązek pochodzących ze źródła światła niespójnego, powstała w wyniku różnic fazowych pomiędzy poszczególnymi falami. Interferencję tą można obserwować za pomocą specjalnej płytki wielowarstwowej. Padająca wiązka składa się z szeregu promieni, z których każdy padając na nią może odbić się na pierwszej warstwie, lub załamać i odbić dopiero na drugiej warstwie. Tak odbite promienie stają się wspólne względem siebie, ponieważ odbicie na granicy ośrodków zmienia fazę fali padającej o π. Płytki takie muszą mieć bardzo małą grubość, tak aby różnica dróg była dobrze określona. Jest to tzw. metoda prążków równego nachylenia.

44. Luneta.

Zasada działania lunety opiera się na zastosowaniu kilku soczewek. Promienie świetlne pochodzące od obiektu S1 zostają skupione za pomocą soczewki w punkcie F, będącym ogniskiem tejże soczewki. W ten sposób powstaje obraz P1 obiektu S1. Skupienie za pomocą soczewki jest możliwe dzięki ugięciu się fali elektromagnetycznej na niej. Jeśli soczewka ma średnicę D, to skupienie się światła odpowiada ugięciu się fali na otworze o takiej średnicy. Rozmycie kątowe obrazu P1 w takiej soczewce wynosi ok. dφ=1,22λ/D. Teraz jeśli mamy oprócz obiektu S1 także jeszcze jeden obiekt S2, który także zostaje skupiony w tej samej soczewce, i jeśli fala biegnąca od tego obiektu biegnie pod kątem dφ = 1,22λ/D to możemy te dwa obiekty odróżnić od siebie. Jest to tak zwana graniczna kątowa rozdzielczość wszystkich przyrządów optycznych. Jak widać, jeśli zwiększa się rozmiar soczewki skupiającej graniczna odległość kątowa maleje, przez co poprawia się zdolność rozdzielcza. Na podobnej zasadzie działa także mikroskop, chociaż w tym wypadku, potrzebne są znacznie większe powiększenia. Dlatego też ustawia się tutaj odległość przedmiotu od obiektywu tak, aby była ona równa ogniskowej obiektywu. Obiektywy natomiast wytwarza się w tym celu, takie aby ich średnica była równa ich ogniskowej. Możemy określić jakiej najmniejszej wielkości dx szczegóły możemy rozróżnić za pomocą mikroskopu: dx/f=1,22λ/D. Czyli nie możemy zobaczyć przedmiotów mniejszych od długości fali elektromagnetycznej.

45. Fale de'Broglie'a

Otóż mechanika klasyczna jest nieprawidłowa przy opisie ruchu cząstek poruszających się z dużymi prędkościami. Przez długi czas nie wiedziano jakie należy zastosować rozwiązanie, aby w adekwatny sposób opisać świat cząstek. Pewne przesłanki do rozwiązania tego problemu pojawiły się w optyce geometrycznej. Otóż jak wiadomo, każdy promień świetlny porusza się po linii prostej, pomiędzy dwoma punktami w przestrzeni. W przypadku gdy na trafi na granicę ośrodków, spełnione jest prawo załamania. W połowie XVIII wieku, światło wyobrażano sobie jako strumień cząstek, czyli że światło miało naturę korpuskularną. Wtedy też sformułowano zasady rządzące optyką geometryczną, między innymi zasadę Fermata opisującą po jakim torze powinno się światło poruszać w przypadku jego przejścia przez granicę dwóch ośrodków. W przypadku uwzględnienia światła jako fali, torami promieni będą kierunki rozchodzenia się takich fali, natomiast powierzchnie, które są prostopadłe do tych kierunków, są powierzchniami tzw. równej fazy. Maupertuls w ok. 100 lat później sformułował w mechanice podobną zasadę wariacyjną. Korzystając z założenia że światło jest falą spełniającą równanie falowe, można dostać tzw. równanie elikonału, wyznaczające tor po jakim powinien poruszać się promień świetlny. Postać równania elikonału ma także równanie Hamiltona - Jacobiego, które z kolei opisuje ruch cząstki materialnej. Nie jest to do końca równanie elikonału tylko funkcja S, określana mianem działania, opisująca zachowanie się cząstki jako punktu materialnego w czasie jednowymiarowego ruchu. Największą niedogodnością w wykryciu fal świetlnych, była bardzo mała długość fali. Jednak, jeśli dostrzeżemy podobieństwa pomiędzy równaniem elikonału a funkcją wyrażającą działanie i jeśli porównamy wielkości takie jak długość fali, czy energia to będziemy na dobrej drodze do dostrzeżenia falowej natury światła. Jednak rewolucja przyszła kiedy to w 1923 roku de'Broglie'a sformułował swoją hipotezę dotyczącą fal materii. Według tej teorii każda cząstka miała ze sobą stowarzyszoną falę o długości λ = h/p, gdzie h oznacza stałą Plancka, a p pęd danej cząstki. Coś tak zaskakującego nie znalazło na początku uznania większej liczby fizyków. Dopiero po pewnym czasie, gdy Schrodinger wraz z Heisenbergiem ogłaszali swoje teorie dotyczące mechaniki kwantowej, teoria de'Broglie'a powróciła do łask. Rok 1919 przyniósł doświadczenia związane z rozpraszaniem elektronów na ciałach krystalicznych, które to wykazały zależność pomiędzy sposobem rozproszenia elektronów, a orientacją ciała krystalicznego. Otóż obserwowano cykliczne zmiany w natężeniu wiązki rozproszonej, swoistego rodzaju maksima i minima. Na początku nie wiedziano jak ten fakt wytłumaczyć i dopiero w 6 lat po tym doświadczeniu ogłoszono, iż jest to efekt dyfrakcji wiązki elektronów na sieci krystalicznej i że efekt ten jest bardzo podobny do dyfrakcji promieni rentgenowskich na krysztale. Wykonano jeszcze szereg innych doświadczeń w których otrzymano podobne wyniki. Wyniki te prowadziły do interpretacji dyfrakcji elektronów na sieci krystalicznej, jako interferencji wiązki elektronów z rzędami atomów, które były odległe od siebie o d. Stąd właśnie powstaje cykliczny obraz interferencyjny w postaci zmian natężenia wiązki rozproszonych elektronów, przy obracaniu kryształu. Dzieje się tak dlatego, że przy obrotach o odpowiedni kąt sieć krystaliczna wraca do położenia takiego, że wiązka elektronów interferuje z rzędami atomów odległymi od siebie o d. W dzisiejszych czasach rozpraszanie elektronów na sieciach krystalicznych ciał stałych jest bardzo ważną metodą badania ich struktury.

46. Równanie Schrodingera.

Skoro wiemy, że każdej cząstce możemy przypisać określoną falę, to w jaki sposób znaleźć taką falą. Metodą pozwalającą na to jest rozwiązanie równania Schrodinegera. Dzięki niemu znajdziemy fale dla danego stanu w przestrzeni, przez co określimy prawdopodobieństwo tego, że cząstka znajdzie się w danym punkcie przestrzeni. Równanie Schrodingera jest postaci:

H ψ = E ψ

Jest to równanie własne pozwalające znaleźć wartości własne energii dla układu opisanego równaniem Hamiltona H, oraz znaleźć powiązane z tymi wartościami własnymi funkcje własne ψ, czyli funkcje falowe. Możemy takie rozwiązanie przeprowadzić dla przypadku cząstki poruszającej się z określonym pędem w kierunku dodatnich wartości osi x. Wtedy poszukiwaną funkcją falową jest:

ψ=A exp[(i/h) (px-Et)]

w równaniu tym i oznacza liczbę urojoną równą pierwiastkowi z -1. Korzystając z teorii de Broglie'a można pęd zapisać w postaci: p = h/λ, to powyższe równanie możemy przepisać do postaci:

ψ = A exp[i(kx - ω t)]

Funkcja ta jest funkcją opisującą falę o wektorze falowym kX. Funkcja pozwala na określenie stanu kwantowego w jakim znajduje się cząstka. Tak więc wiemy już jak obliczyć i jak wygląda funkcja falowa dla danej cząstki. Jednak jaki jest sens fizyczny takiej fali. Otóż pozwala ona określić prawdopodobieństwo cząstki w danym punkcie. A właściwie to kwadrat modułu funkcji falowej, jest wartością prawdopodobieństwa znalezienia cząstki w określonym punkcie przestrzeni.

P = | ψ |2 = ψ ψ*

Z faktu, że jest to prawdopodobieństwo, a prawdopodobieństwo znalezienia cząstki w całej przestrzeni musi być równe 1, wynikają tzw. warunki normalizacyjne. Otóż całka z kwadratu modułu funkcji falowej po całej przestrzeni musi być równa 1. Dla przypadku kiedy dana funkcja falowa opisuje więcej niż jedną cząstkę, tak jest w przypadku fotonów. To wielkość ψ ψ* określa gęstość cząstek. Gęstość fotonów w dalszej kolejności decyduje o gęstości promieniowania. A natomiast gęstość promieniowania decyduje o natężeniu światła. Czyli w skrócie natężenie światła zależy od gęstości fotonów, czyli od kwadratu modułu funkcji falowej | ψ |2. Stąd widać że promieniowanie elektromagnetyczne jest zależne od funkcji falowej i może być opisane za pomocą fali.

47. Zasada nieoznaczoności Heisenberga

Jak wynika z rozwiązania równania Schrodingera dla cząstki swobodnej o energii E i pędzie p poruszającej się w kierunku dodatnich wartości x, funkcja falowa opisująca taką cząstkę jest postaci:

ψ = A exp[i(kx - ω t)]

W przypadku gdy amplituda jest rzeczywista i jest stała to P = | ψ |2 = ψ ψ* = A2. Z postaci funkcji falowej wynika, że cząstka nią opisana może znajdować się w każdym punkcie przestrzeni od -¥ do +¥. Jednak to że cząstkę widzimy jako zlokalizowaną w określonym miejscu przestrzeni, a nie skaczącą po całym obszarze, zależy bezpośrednio od prawdopodobieństwa znalezienia cząstki w danym miejscu. Prawdopodobieństwo to mówi nam o większym lub mniejszym stopniu zlokalizowania cząstki. Funkcja falowa dla cząstki ma postać paczki falowej. Dzięki temu możemy określić rozkład gęstości prawdopodobieństwa znalezienia cząstki w przestrzeni. Prędkość fazowa takiej paczki falowej wynosi:

Vfaz =ω/k=E/p

Gdy jako energii użyjemy:

E=p2/2m

To prędkość fazowa będzie wynosić Vfaz = v/2

W przypadku, gdy użyjemy energii postaci E = mc2, to prędkość fazowa będzie wynosić Vfaz = c2/2. Okazuje się, że faktycznie funkcje falowej realnych cząstek mają postać paczek falowych.

Zasady nieoznaczoności, Heisenberga:

Δx ΔpX = h

ΔE Δt = h

Podobnie wyglądają powyższe związki dla pozostałych składowych. Zasada nieoznaczoności mówi nam o tym, że im lepiej zlokalizujemy cząstkę w przestrzeni, czyli im lepiej określimy jej odpowiednią współrzędną, to tym większe dostaniemy rozmycie pędu w tym kierunku. To samo się tyczy energii i czasu cząstki. Zasada nieoznaczoności to nie tylko teoretyczny mechanizm, to faktycznie obecne w przyrodzie prawo. Zasada ta decyduje min. o czasie życia poziomów energetycznych w atomie. Otóż, jako że stan podstawowy atomu jest ściśle określony, to czas życia takiego stanu jest praktycznie dowolny. Także foton podlega działaniu zasady nieoznaczoności. W wyniku działania zasady nieoznaczoności nie możemy przeprowadzić jednoczesnego pomiaru położenia cząstki oraz jej pędu. Także nie możemy określić dokładnie energii cząstki i jej czasu życia.

Naukowcy spierają się, co do skutków zasady nieoznaczoności. Jedną z jej implikacji jest istnienie pewnej elementarnej długości Plancka, która wyznacza granice pomiarów. Jej wartość szacuje się na 10-35 metra. Wartość tą można interpretować w ten sposób, że każda inna długość jest jej wielokrotnością. Idąc dalej niektórzy naukowcy uważają, że czas też nie płynie w sposób ciągły, lecz zmienia się skokowo. Na jedną sekundę przypada ok. 5 x 1044 elementarnych kroków, w których zmienia się stan naszego otoczenia. Odwrotność tej liczby określa się jako czas Plancka. Jednak długość Plancka i czas Plancka znajduje, się daleko poza zasięgiem dokładności pomiarów nawet w największych akceleratorach cząstek

48. Cząstka w stanie związanym.

O stanie związanym mówi się w przypadku układu dwóch cząstek przyciągających się wzajemnie. Na skutek tego całkowita energia tych dwu cząstek jest mniejsza niż w przypadku, gdy cząstki te były w osobności. Efektowi temu towarzyszy także spadek całkowitej masy układu. A cały układ jest opisywany pojęciem zredukowanej masy, masa ta znajduje się w polu, które oddziałuje na cząstki. Pole to przebiera postać dołu potencjału. Przykładem tutaj może być atom, w którym jądro jest w centrum pola oddziaływań, a elektron jest masą zredukowaną poruszającą się w tym polu. Dla przypadku, w którym mamy do czynienia z dwoma atomami łączącymi się w cząsteczkę, masą zredukowaną jest masa połowy jednego z tych atomów. To powoduje, że wzajemne odległości tych atomów są równe.

49. Promieniowanie Roentgena

Odkryte zostało w 1895 r. przez W. K. Roentgena. Za to odkrycie dostał w 1901 r. nagrodę Nobla. Roentgen odkrył to promieniowanie gdy badała promieniowanie katody. W czasie swoich badań z rurą katodową znajdował się w pobliżu ekran powleczony platynocyjankiem baru. Roentgen spostrzegł, iż ekran ten świeci gdy rura katodowa działała. Zauważywszy to zjawisko zaczął je bliżej badać zasłaniając katodę różnymi materiałami, takimi jak klisza fotograficzna, czy czarny papier. Jednak w każdym przypadku ekran nadal świecił. Podczas dalszych badań stwierdził, iż promieniowanie które obserwował przechodzi także przez inne ciała, które dla zwykłego światła są nieprzezroczyste. Odkryte przez siebie promieniowanie nazwał promieniami X. W dzisiejszych czasach promieniowanie X jest wytwarzane przez 2 urządzenia, specjalne lampy. Jedną z nich jest tzw. jonowa lampa rentgenowska. Lampa ta to nic innego jak niewielka, (średnica ok. kilku - kilkunastu cm) szklana bańka, w której znajduje się gaz będący pod niskim ciśnieniem rzędu dziesiątych części Pa. W takiej bańce znajdują się trzy elektrody - anoda A, katoda K i antykatoda T. Anoda jest bezpośrednio połączona z antykatodą, w ten sposób umożliwiając przepływ elektronów. Katoda ma natomiast kształt wklęsłej miseczki. Lampa działa w ten sposób, że na początku ustala się bardzo wysokie napięcie na układzie anoda - antykatoda, napięcie rzędu dziesiątek tysięcy Woltów. W szklanej bańce znajdują się jony dodatnie, które rozpoczynają bombardowanie katody. Wskutek tego z katody wyzwalane są elektrony. Elektrony te z racji wklęsłego kształtu katody, tworzą zbieżny strumień który pada na mały ściśle określony obszar antykatody. Gdy elektron uderza w powierzchnię antykatody, zostaje wyhamowany ponieważ trafia na atomy pierwiastka z którego zbudowana jest antykatoda. Wskutek hamowania elektrony tracą swoją energię, wypromieniowując ją w postaci promieniowania hamowania - promieniowania roentgena. Tak powstałe fotony mają swoją określoną energię i częstotliwość, tym większą im szybciej elektron zostaje wyhamowany. Maksymalna energia jest wypromieniowana wtedy gdy elektron zostaje całkowicie wyhamowany przez atom. Maksimum tej energii i jednocześnie graniczną długość fali promieniowania określa pole elektryczne w jakim przyspieszane są elektrony.

50. Stan układów termodynamicznych

Stan termodynamiczny ciała - stan, który można określić jednoznacznie, jeśli korzystając z tego samego rodzaju, można odtworzyć to ciało w zupełnie innym miejscu, tak aby można było zbadać jego właściwości termodynamiczne. Tak więc do określenia stanu termodynamicznego ciała, nie jest potrzebna wiedza dotycząca własności substancji z której jest to ciało zbudowane, nie jest wymagana znajomość takich parametrów substancji jak współczynnik ciepła, współczynnik przewodnictwa cieplnego, a nawet nieistotny jest kształt substancji. Natomiast stan termodynamiczny ciała fizycznego, układu termodynamicznego lub substancji jest określony przez tzw. parametry stanu, czyli pewny zbiór możliwych do zmiany właściwości fizycznych. Stan termodynamiczny można zmienić poprzez zmianę parametrów stanu.

Parametry intensywne - parametry lokalne - są to parametry, które mogą być określone zarówno dla ciała jako całości, ale także dla fragmentu danego ciała. Przykładami takich parametrów są ciśnienie i temperatura. Parametry te po przypisaniu ich do każdego fragmentu ciała mogą tworzyć tak zwane pole, tak jak w przypadku pola temperaturowego. Jeśli wszystkie punkty danego ciała, mają jednakowe wartości parametru, ciało takie jest jednorodne pod względem tego parametru.

Parametry ekstensywne - parametry globalne - są one określane dla ciała jako całości, dla całej jego objętości, przy czym zależą bezpośrednio od ilości substancji w ciele. Jeśli są określane dla całego ciała to znaczy że nie mogą być jednakowe także dla fragmentów substancji. Przykładami takich parametrów są objętość i energia wewnętrzna, a także entropia. Parametry te można dodawać, wtedy wartość ogólna parametru dla całego układu jest sumą parametrów dla poszczególnych części układu.

Parametry właściwe - są to parametry, które charakteryzują rodzaj substancji, są to szczególny rodzaj parametrów intensywnych. Wartość parametrów ekstensywnych jest zawsze proporcjonalna do ilości substancji w ciele. W przypadku substancji jednorodnej przypisuje się parametry właściwe będące wartościami parametrów ekstensywnych, jakie przypadają na ilość substancji. Dla przypadku substancji które są niejednorodne parametry właściwe określa się jako pochodne parametrów ekstensywnych na ilość substancji. Przykładami parametrów właściwych są entropia właściwa, czy objętość właściwa.

Stan równowagi trwałej - stan w jakim może być układ, polegający na bardzo niewielkich zmianach układu, pod wpływem działania bardzo niewielkich czynników. Stan taki powstaje w przypadku, gdy otoczenie nie oddziałuje na układ, lub w przypadku, gdy te oddziaływania wzajemnie się znoszą.

51. Ruchy Browna

Brown w 1827 roku podczas obserwacji pod mikroskopem mikroskopijnych cząstek zawiesiny w wodzie, zauważył, że poruszają się one w dosyć chaotyczny sposób przypominający ruchu organizmów żywych mikroskopijnych rozmiarów. Jednak do początku XX wieku zjawisko to nie zostało wyjaśnione. Dopiero w 1905 roku Einstein i Smoluchowski opisali ruchy takich cząstek, które dzisiaj są określane mianem Ruchów Browna. Według tej teorii cząstka taka jest swoistego rodzaju mikropyłkiem, podobnym do molekuły gazu. W czasie swej obecności w innym ośrodku jakim była woda, pyłek ten nieustannie jest uderzany przez molekuły gazu, przez co porusza się w sposób chaotyczny we wszystkich kierunkach. Energia jaką posiada po uśrednieniu wynosi 3kT/2, natomiast kwadrat przesunięcia po uśrednieniu x2 = kTt/3πhρ. Jest to bardzo ważna reguła ruchów Browna, głosząca, że średni kwadrat przesunięcia cząstki jest proporcjonalny do czasu jej ruchu. Ruchy Browna są bardzo ważnym zjawiskiem w przyrodzie, ponieważ powodują one powstawanie różnego rodzaju fluktuacji termodynamicznych, tzw. szumów cieplnych. Szumy te są bezpośrednią przyczyną ograniczonej zdolności pomiarowej przyrządów. Dokładność tą można zwiększać poprzez stosowanie lepszych materiałów z których są zbudowane. Jednak w wielu przypadkach nie da się na tym polu już osiągnąć większej dokładności, dlatego też wtedy stosuje się chłodzenie układów mające na celu wyeliminowanie szumów cieplnych. Przykładem takich problemów spowodowanych przez ten rodzaj szumów jest ograniczona dokładność różnego rodzaju mierników elektrycznych. Szumy te wynikają z drgań sieci krystalicznej przewodników, zbudowanej z jonów, a także poprzez sam ruch cieplny elektronów poruszających się w przewodnikach. Występowanie takich ruchów przejawia się w powstawaniu krótkich ostrych impulsów, które na miernikach mogą być obserwowane jako cienkie szpilki.

52. Rozpad β

W przyrodzie obserwujemy procesy rozpadu promieniotwórczego, który polega na rozpadaniu się nietrwałych jąder z równoczesną emisją określonych cząstek. Jednym z takich rozpadów jest rozpad β. W procesie tym jądro atomowe rozpada się emitując przy tym elektrony lub pozytony oraz neutrina. Cząstka neutrino jest cząstką bardzo ciekawą i w obecnym czasie stanowi obiekt żywego zainteresowania fizyków z całego świata. Jest to cząstka która praktycznie nie oddziałuje z materią, głównie z powodu jej bardzo małej masy, która według ostatnich badań nie może być znacząco różna od 0. Podczas rozpadu beta powstała nadwyżka energii zostaje rozdzielona na energię kinetyczną elektronu, czyli cząstkę β-, oraz na energię neutrina. W rozpadzie beta energia stanu początkowego ma postać: M(Z,N) c2, natomiast energia stanu końcowego: M(Z+1,N-1) c2.

53. Rozszczepienie jądrowe.

Proces rozszczepienia jądrowego polega na rozerwaniu jądra atomowego z jednoczesnym wydzieleniem energii, równej energii wiązania tego jądra. Pierwszym odkrytym procesem rozszczepienia było rozszczepienie jądra uranu. Proces ten odkryto w roku wybuchu II wojny światowej, za pomocą bombardowania neutronami jąder uranu. Oprócz uranu rozszczepieniu ulegają także inne ciężkie izotopy. W wyniku procesu rozszczepienia jądra atomowego, dzieli się ono na dwa fragmenty - pierwiastki najczęściej promieniotwórcze. Podczas procesu rozszczepienia, energia jaka jest uwalniana wynosi ok. 200 MeV. Jaki jest sam mechanizm powodujący rozszczepienie. Otóż pochłonięcie neutronu powoduje wzbudzenie jądra do energii wyższej o ok. 5 MeV. Pochłonięcie takie kropli materii jądrowej powoduje, że jądro zaczyna się "rozciągać", a to w połączeniu z kwantowym efektem tunelowanie może spowodować, że siły kulombowskie odpychające oba fragmenty przewyższą siły jądrowe je przyciągające. W wyniku rozszczepienia powstają dwa nowe jądra i co najważniejsze emitowane są wolne neutrony. Te neutrony mogą spowodować kolejne reakcje rozszczepienia, co prowadzi dalej do lawinowych rozszczepień i olbrzymich sumarycznych energii uwalnianych. Możliwym jest też, że jądro samorzutnie ulegnie rozszczepieniu, jednak z braku czynnika wzbudzającego, jest to proces o niskim prawdopodobieństwie zajścia.

54. Reaktor jądrowy.

Dokładny ilościowy opis procesów zachodzących w reaktorze jądrowym jest dosyć złożony. Wymaga on bowiem uwzględnienia wszelkiego ruchu i gęstości neutronów. Rozwiązanie tego problemu sprowadza się do rozwiązania kilku równań w wyniku czego można otrzymać rozkład gęstości neutronów w przestrzeni. Bardzo ważnym zagadnieniem jest znajomość takiego rozkładu, ponieważ decyduje on o bezpiecznym przeprowadzaniu reakcji rozszczepień. Zasadniczymi elementami z jakich zbudowany jest reaktor są: paliwo jądrowe, moderator, substancja schładzająca, osłona ze specjalnego rodzaju betonu, reflektory oraz kanały naświetleniowe. Sercem każdego reaktora jądrowego jest rdzeń jądrowy, zawierający pierwiastek będący paliwem jądrowym, czyli 235U. Moderator służy do spowalniania neutronów, jednak do takich energii aby mogły spowodować rozszczepienia.

55. Odpady promieniotwórcze

Podczas reakcji rozszczepienia, które zachodzą min. w reaktorach jądrowych produkowane są pierwiastki promieniotwórcze. Pierwiastki te mają różne czasy połowicznego rozpadu, wahające się od kilku milisekund do nawet ok. wieku. Ich zagrożenie dla człowieka także jest zróżnicowane. Zasady postępowania z takimi odpadami są następujące. Odpady promieniotwórcze przez pierwsze kilka lat przechowuje się w okolicach reaktora, po to aby wszelkie pierwiastki o krótkich czasach życia, mogły się całkowicie rozpaść. Jest to tzw. etap studzenia odpadów. Po tym czasie pozostałe odpady zbiera się i umieszcza w specjalnie do tego celu zbudowanych pojemnikach, szczelnych komorach. Część natomiast z nich nadaje się do ponownego użytku. Obecnie prowadzi się badania nad metodą utylizacji odpadów promieniotwórczych, polegającej na oświetlaniu tychże. Powstała energia w wyniku rozszczepień przeprowadzanych w reaktorach jądrowych, jest obecnie pomimo faktu istnienia tak niebezpiecznych odpadów (z którymi ludzie nauczyli już sobie odpowiednio radzić) jedną z najczystszych metod uzyskiwania energii.