Masa ciała jest wielkością skalarną. Ciężar ciała to natomiast wielkość wektorowa równa sile, z jaką nasza planeta przyciąga to ciało. Kierunek ciężaru jest zgodny z kierunkiem siły grawitacyjnej, czyli do wnętrza Ziemi.
Zależność między masą a ciężarem można zapisać na podstawie drugiej zasady dynamiki Newtona. Wygląda ona następująco:
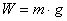
gdzie: W to ciężar, m - masa ciała a g - przyspieszenie ziemskie.
Jak wykazują badania wartość przyspieszenia ziemskiego jest różna w różnych miejscach na Ziemi. Przyspieszenie ziemskie osiąga największą wartość na biegunie, a najmniejszą na równiku. Można z tego wnioskować, że będzie się także zmieniał ciężar ciała.
Masa jest niezmienną wielkością charakteryzującą dane ciało. Natomiast ciężar zmienia się w zależności od odległości od środka Ziemi. Jeżeli do pomiarów ciężaru ciała zostałaby użyta waga sprężynowa, to jej wskazania dla masy 1 kilograma byłyby różne w różnych punktach na Ziemi.
Przyspieszenie ziemskie ma stałą wartość dla wszystkich ciał zlokalizowanych w danym miejscu. Tą własność wykorzystuje waga analityczna, która tak naprawdę porównuje dwie siły. Jeżeli na jednej z szalek zostanie położone ciało, którego siła nacisku na szalkę będzie równa sile nacisku wzorca o masie 1 kg położonego na drugiej szalce to można powiedzieć, że masa tego ciała wynosi 1 kilogram. I wskazanie takiej wagi nie będzie się zmieniało w zależności od miejsca na powierzchni Ziemi.
Tak więc wagi szalkowe mogą być używane do porównywani mas ciał.
W tych obszarach , których przyspieszenie grawitacyjne jest równe zero ciężar ciała również jest zerowy mimo, że masa ciał jest taka sama jak na powierzchni Ziemi. Dlatego możliwe byłoby w takiej przestrzeni podnoszenie przedmiotów o olbrzymich ciężarach. Natomiast kopnięcie w taki obiekt byłoby odczuwalne tak samo jak na powierzchni Ziemi, ponieważ masa się nie zmieniła.
Należy wprowadzić rozróżnienie między masą grawitacyjną a masą bezwładną. Konsekwencją posiadania przez ciało masy grawitacyjnej jest istnienie przyciągania grawitacyjnego między ciałem a Ziemią. Wartość tej siły dana jest wzorem:
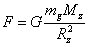
gdzie m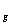 to masa grawitacyjna ciała, a wielkości z indeksem "z" dotyczą odpowiednio masy i promienia Ziemi.
to masa grawitacyjna ciała, a wielkości z indeksem "z" dotyczą odpowiednio masy i promienia Ziemi.
Natomiast, gdy np. chcemy wprawić w ruch ciało spoczywające na tak gładkiej powierzchni, że można pominąć siły tarcia, wymaga to pewnego nakładu pracy. Siły ciężkości nie odgrywają tu żadnej roli. Natomiast ta konieczność użycia siły związana jest z tzw. masą bezwładną.
Wyniki licznych doświadczeń polegających m.in. na pomiarach przyspieszeń ciał spadających w próżni dowiodło, że te przyspieszenia są sobie równe i wynoszą g. Z tego wynika, że masa bezwładna jest równa masie grawitacyjnej. Zależność ta została nazwana zasadą równoważności.
Odkrycie to doprowadziło do sformułowania przez Einsteina ogólnej teorii względności.


