Wektor jest uporządkowaną parą punktów A i B, przy czym punkt A to początek wektora, natomiast punkt B to jego koniec.
Patrząc na interpretacje geometryczną wektora, możemy powiedzieć, że jest on skierowanym odcinkiem AB leżącym na prostej.
[A, B] = - [B, A]
Istnieje parę sposobów notowania wektora.
Składowe wektora to różnice współrzędnych końca wektora i jego początku:
Bx - Ax, By - Ay, Bz - Az,
długość wektora to długość odcinka AB.
Kierunek wektora, to kierunek prostej, w której jest zawarty, natomiast zwrot określa kolejność punktów końcowego i początkowego: A i B.
Aby pokazać jak przebiega droga od jednego do drugiego punktu, nie wystarczy podać współrzędnych tych punktów, trzeba jeszcze określić, który jest pierwszy, a który drugi.
Pierwszy punkt nazywany jest początkiem wektora, a drugi jego końcem. Odległość jaka dzieli początek i koniec wektora, nazywana jest długością wektora.
Oznaczając wektor o początku w punkcie A i końcu w punkcie B używamy symbolu: 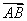
Wektor, który ma początek i koniec w tym samym punkcie, nazywa się wektorem zerowym.
Dwa niezerowe wektory są równoległe, jeżeli proste, które są wyznaczone przez wektory leżą równolegle.
Wektory równoległe mają ten sam kierunek.
Dwa wektory, które mają ten sam kierunek mogą mieć zgodny lub przeciwny zwrot.
Dwa wektory są o zgodnym zwrocie, jeśli nie leżą na jednej prostej, ale leżą w półpłaszczyźnie, której krawędź jest prostą, która przechodzi przez początki wektorów.
Dwa wektory są o przeciwnym zwrocie, jeśli nie leżą na jednej prostej, ale jeżeli są położone w półpłaszczyznach, które się uzupełniają, której krawędź jest prostą, która przechodzi przez początki wektorów.
Dwa równoległe wektory, które leżą w jednej prostej, są o zgodnym zwrocie, jeżeli półprosta, która jest wyznaczona przez pierwszy z nich, jest zawarta w półprostej, która jest wyznaczona przez drugi wektor,
zaś maja przeciwny zwrot, jeżeli żadna z tych półprostych, które są wyznaczone przez nasze wektory nie jest zawarta w drugiej.
Równość wektorów
Dwa wektory niezerowe są równe, gdy mają taką samą długość, kierunek i zwrot.
Dwa równe wektory mogą mieć początki w różnych punktach, czyli różne punkty zaczepienia. Znaczy to, że w dowolnym punkcie możemy utworzyć, który jest równy danemu.
Możemy to zrobić w następujący sposób:
- wybrać dowolny punkt
- poprowadzić przez niego prostą, która będzie równoległa do naszego danego wektora
- odmierzyć od tego punktu długość wyjściowego wektora z dowolnej jego strony
- jako koniec wybrać z tych dwóch punktów ten, aby wektory miały taki sam zwrot.
Dodawanie wektorów
Mamy dane dwa wektory, jeden zaczepiony w punkcie A, drugi w punkcie B. Nazwiemy je kolejno AC i BD.
Zdefiniujmy wektor AE jako sumę wektorów AC i BD, ponieważ wynikiem dodawania wektorów jest wektor. Wektor ten można zaczepić w dowolnym punkcie, jest on równy sumie wektorów i jest jednoznacznie wyznaczony z dokładnością do punktu zaczepienia.
Reguła równoległoboku:
Dla wektorów, które nie mają takiego samego kierunku można zastosować regułę równoległoboku.
Polega ona na tym, że jeden wektor pozostawiamy w tym samym miejscu, w którym był, niech to będzie wektor AC. Drugi przesuwamy nie zmieniając jego kierunku, ani zwrotu w ten sposób, aby oba wektory miały początek w tym samym punkcie, niech to będzie wektor BD. Następnie na końcu wektora AC zaczepiamy wektor identyczny jak BD, tylko przesunięty oraz na końcu wektora BD wektor identyczny jak AC, tylko przesunięty. W ten sposób końce wektorów zetkną się w jednym punkcie, nazwijmy go E. W taki oto sposób otrzymaliśmy równoległobok, którego przekątna AE jest naszym szukanym wektorem, czyli sumą wektorów AC i BD. Jego początek jest w punkcie A, a koniec w punkcie E.
Odejmowanie wektorów
Chcąc odjąć wektory, postępujemy podobnie jak przy dodawaniu, tylko dodajemy wektor przeciwny, czyli:
AB – CD możemy odjąć w następujący sposób: AB + (- CD).
Wektor przeciwny do danego wektora AB to wektor BA. Ma on tą samą długość, taki sam kierunek różni ich tylko przeciwny zwrot.


