Minimalizacja funkcji logicznych

Wstęp

W informatyce często staje się przed problemem minimalizacji funkcji logicznych. Zanim jednak przejdziemy do omówienia tego zagadnienia, musimy przejść przez wszystkie definicje, które powiedzą nam, czym tak naprawdę jest funkcja logiczna.

Zagadnienie związane z minimalizacją funkcji logicznych można sformułować na wiele sposobów. Przede wszystkim jest to problem, jak uprościć funkcję logiczną tak, by jej zapis był jak najbardziej zwięzły. Innymi słowy, problem sprowadza się także do znalezienia funkcji minimalnej, która pod względem logicznym będzie równoważna naszej wyjściowej funkcji.

Jednak, jakie są kryteria, które mówią, jak bardzo funkcja jest skomplikowana? Całe szczęście jest to określone. Mianowicie, wprowadzone zostało pojęcie, które mówi o współczynniku skomplikowania funkcji. Najczęściej definiuje się go jako ilość spójników logicznych w zapisie funkcji, oczywiście w zależności od ilości zmiennych funkcja będzie mniej lub bardziej skomplikowana. Jednak zawsze daną funkcję da się zapisać jako funkcję o dużo większym skomplikowaniu, używając do tego tak zwanych iloczynów pełnych. Dla przykładu, funkcję trzech zmiennych można zapisać jako

f(x,y,z) = ~x~y~z + ~x~yz + ~xyz + xy~z + xyz

lub jako

f(x,y,z) = xy + ~x~y + ~xz

Obie funkcje są równoważne, to znaczy dla odpowiednich wartości zero lub jeden argumentów przybierają te same wartości.

Istnieje wiele różnych metod minimalizacji funkcji logicznych. Zasadniczo można je sklasyfikować w dwóch grupach. Pierwsza grupa to tak zwane metody algebraiczne, druga to metody algorytmiczne.

Zaprezentuję przykład metody algebraicznej, która bazuje głównie na prawach de Morgana dla funkcji logicznych.

f(x,y,z) = xyz + xy~z + ~x~yz + ~xyz = xy(z + ~z) + ~xz(~y + y) = xy + ~xz

Jak widać, tego typu przekształcenia są raczej żmudne i łatwo jest się pomylić. Dlatego opracowano wiele metod algorytmicznych, dzięki którym minimalizacja jest łatwiejsza. Dwie z nich postaram się omówić - są to metoda Quine'a-McCluskeya oraz metoda tablic Karnaugh.

Metoda Quine'a-McCluskeya

Pierwszą metodą, jaką chcę tutaj omówić jest metoda Quine'a-McCluskeya. Chociaż z początku jest to dość skomplikowana metoda, okazuje się, że łatwo jest nie tylko używać jej ręcznie, ale przede wszystkim zaimplementować ją na komputerze. Jest to metoda, która może być stosowana do funkcji o dużej liczbie zmiennych, ponieważ druga z metod, metoda tablic Karnaugh, jest ciężka do używania, jeśli mamy funkcję więcej niż czterech zmiennych.

Aby przeprowadzić przykładową minimalizację metodą Quine'a-McCluskeya wprowadźmy pojęcie iloczynów pełnych.

Iloczynem pełnym nazywamy logiczny iloczyn wszystkich zmiennych funkcji, w którym zmienne są zanegowane lub nie. Przykładowo, jeśli funkcja jest czterech zmiennych w, x, y, z, iloczyn pełny to na przykład w~xy~z.

Iloczyny pełne układa się w kolejności. Wyznaczają ją liczby dwójkowe odpowiadające iloczynowi. Zmienna zanegowana jest wartością zero, zmienna niezanegowana jest wartością 1. Poprzednio wymieniony iloczyn pełny ma wartość 1010, czyli dziesięć. Jest to dziesiąty w kolejności iloczyn pełny czterech zmiennych.

Funkcję logiczną zawierającą iloczyny pełne można zapisać skrótowo jako sumę kolejnych iloczynów pełnych:

f(w,x,y,z) = Σ(5,7,8,9,10,11,13,15)

Oznacza to, że funkcja jest sumą iloczynów pełnych o konkretnych numerach.

Zminimalizujmy tę funkcję metodą Quine'a-McCluskeya.

W pierwszym kroku wypisujemy numery iloczynów pełnych w czterech (bo 4 zmienne) grupach, które to różnią się między sobą ilością jedynek.

8 1000 - jedna jedynka

5 0101 - dwie jedynki

9 1001 - dwie jedynki

101010 - dwie jedynki

7 0111 - trzy jedynki

11 1011 - trzy jedynki

13 1101 - trzy jedynki

15 1111 - cztery jedynki

Teraz kolejnym krokiem jest iteracja. Porównujemy pomiędzy sobą każdy z każdym elementy z sąsiednich grup. Jeśli elementy różnią się tylko na jednej pozycji, należy "skleić" je ze sobą i w miejscu, gdzie się różniły stawia się kreseczkę. Oczywiście jest to wykorzystanie jednego z podstawowych praw logicznych, mianowicie xy + x~y = x.

W kolejnym kroku przepisujemy tabelę tak, by elementy w poszczególnych grupach znów różniły się tylko o jedną jedynkę.

W naszym przykładzie będzie to wyglądało tak:

8-9 100-

8-10 10-0

5-7 01-1

5-13 -101

9-11 10-1

9-13 1-01

10-11 101-

7-15 -111

11-15 1-11

13-15 11-1

Iterujemy poprzedni krok tak, aby uzyskać kombinację, która nie da się już uprościć. W naszym przypadku dzieje się tak już w trzecim kroku. Inne kombinacje dają te same wyniki.

8-9-10-1110--

5-7-43-15 -1-1

9-11-13-15 1-1-

Kiedy już dojdziemy do takiego rezultatu, musimy odczytać wynik. W tym celu należy stworzyć tak zwaną siatkę Quine'a-McCluskeya.

Ostatnia kolumna jest odpowiednikiem przedostatniej, tylko zapisanej jako zmienne.

Teraz należy wybrać takie elementy, aby "pokryć" wszystkie iloczyny pełne. Optymalnym wyborem będzie u nas:

Zatem nasza zminimalizowana funkcja będzie miała postać

f(w,x,y,z) = w~x + xz.

Oczywiście rozwiązaniem jest także

f(w,x,y,z) = w~x + xz + wz,

jednak jak widać jest to funkcja o większym współczynniku skomplikowania.

Ta część minimalizacji metodą Quine'a-McCluskeya opiera się na następującym fakcie. Każde połączenie sum logicznych czy iloczynów logicznych takich jak x₁x₂~x₃+ x₁x₂x₃ = x₁x₂ są tak zwanymi IMPLIKANTAMI. Dlatego można zapisać każdą funkcję logiczną sztucznie jako sumę iloczynów pełnych, rozszerzając poszczególne elementy tak jak to podano wyżej. Wprowadza się także definicję implikantu prostego, który jest implikantem pewnej formuły, i jednocześnie jest najprostszy pod względem skomplikowania.

Jeśli zatem mamy implikanty proste odpowiadające naszej funkcji, to suma niektórych lub wszystkich z nich jest równoważna wyjściowej funkcji. Wyboru dokonuje się w ten sposób, aby możliwa była reprezentacja każdego z iloczynów pełnych poprzez jeden z implikantów, tak jak to robiliśmy w drugiej części metody Quine'a-McCluskeya. Oczywiście, musimy wybrać tak, by liczba wykorzystanych implikantów nie była wysoka, ściślej - by była to możliwie najmniejsza ilość. Wszystko oczywiście po to, by zminimalizowana funkcja posiadała jak najmniejszy współczynnik skomplikowania.

Metoda tablic Karnaugh

Inną algorytmiczną metodą upraszczania funkcji logicznych jest metoda tablic Karnaugh, zwana także metodą Veitcha. Stosuje się tutaj diagramy, przypominające kwadratowe lub prostokątne tablice. W zależności od ilości zmiennych, od których jest uzależniona funkcja, tablica ta jest większa. Konkretnie dla n zmiennych mamy 2ⁿ pól w tablicy, dlatego dla wielu zmiennych ta metoda jest dość żmudna i raczej niemożliwa do przeprowadzenia. Jednak w ręcznym minimalizowaniu funkcji do czterech-pięciu zmiennych jest chyba wygodniejsza niż metoda Quine'a-McCluskeya.

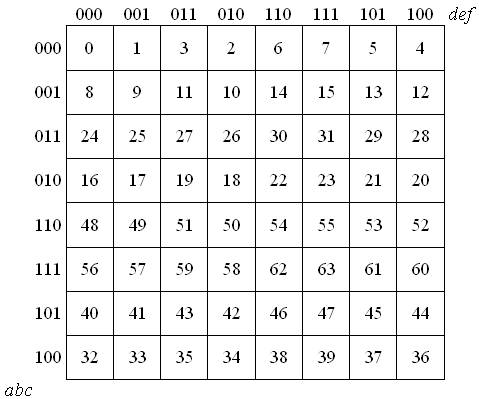
Tablica Karnaugh wygląda w sposób następujący. Przede wszystkim, każde z pól posiada swój określony numer, który odpowiada numerowi iloczynu pełnego. Często pomija się ten numer, ponieważ używa się łatwych do zapamiętania tablic, jednak warto zawsze w rogu komórki pisać, jaki numer odpowiada danemu polu, zwłaszcza na początku.

Oprócz numeru komórki w danym polu wprowadza się jeden z trzech symboli. Pierwszy z nich to symbol 1, kiedy w zapisie funkcji znajduje się iloczyn pełny oznaczony numerem komórki, 0, kiedy danego iloczynu pełnego nie ma w zapisie funkcji. Możliwe jest także, że niektóre iloczyny pełne są tak zwanymi iloczynami nieistotnymi, gdzie nie jest ważne, jaka wartość funkcji jest dla niektórych wartości argumentów. Wówczas w kratce tablicy Karnaugh stawia się trzeci symbol - może to być na przykład znak *. 

Oto przykładowa tablica Karnaugh z opisem Veitcha:

Wariant z numerami iloczynów, często używany jako wzorzec i diagram pomocniczy, wariant z pełną funkcją logiczną oraz z funkcją niepełną, gdzie mamy do czynienia z iloczynami nieistotnymi:

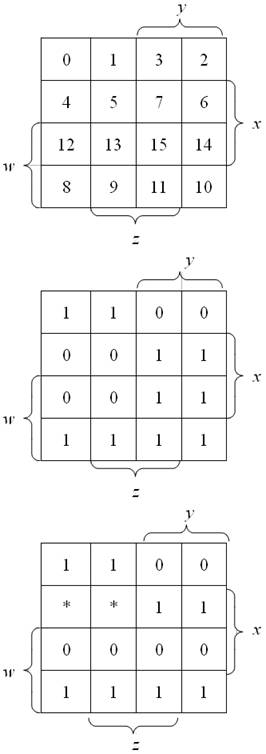Każdą kratkę tablicy Karnaugh, jak wiemy, można utożsamić z konkretnym wektorem zmiennych funkcji, czyli z konkretnym iloczynem pełnym. Inaczej możemy powiedzieć, że każda kratka posiada swój unikalny adres, który można odczytać dzięki opisowi wokół tablicy. I tak na przykład kratka o numerze 15 ma adres wxyz, natomiast kratka o numerze 5 ~wx~yz.

Można zapamiętać, jak wygląda przykładowa tablica Karnaugh. Jednak należy zdawać sobie sprawę, że jest to jedna z wielu możliwości. Istnieją pewne sposoby, które pozwalają stworzyć taki diagram.

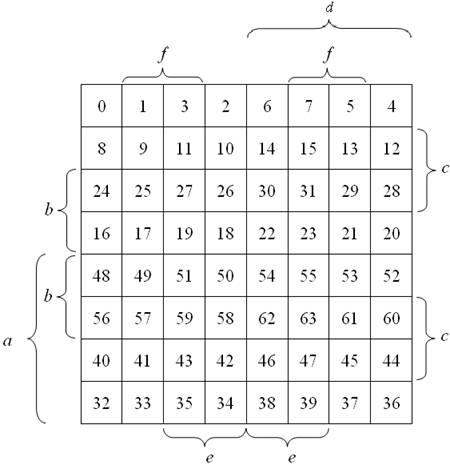
Przede wszystkim, należy pamiętać, że cały prostokąt jest odpowiednikiem sumy wszystkich iloczynów pełnych. Równie dobrze można też przyjąć, że jest to iloczyn pełnych sum.

Zawsze jednej ze zmiennych odpowiada jedna druga powierzchni kwadratu. Zatem dla diagramu o ośmiu kratkach każda z trzech zmiennych posiada cztery pola dla siebie i cztery dla swojej negacji. Oczywiście należy pamiętać o tym, że każdej zmiennej musi odpowiadać inna powierzchnia.

Kolejnym krokiem jest stwierdzenie, jakie iloczyny pełne są wyznaczane przez poszczególne kratki. Adres kratki odczytuje się w ten sposób, że każda zanegowana zmienna w adresie jest zerem, każda niezanegowana jest jedynką. Oczywiście trzeba ustalić pewną kolejność zmiennych. Jeśli uznajemy, że kratka ma być adresem nie iloczynu, a sumy pełnej, adres kratki określa się tak samo.

Najczęściej używa się następujących uporządkowań dla tablic Karnaugh (kolejność zmiennych od a):

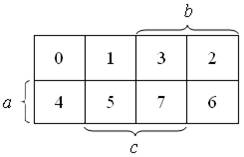
Tablica dla dwóch zmiennych:

Tablica dla trzech zmiennych:

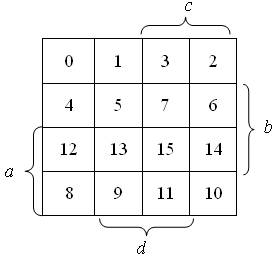
Tablica dla czterech zmiennych:

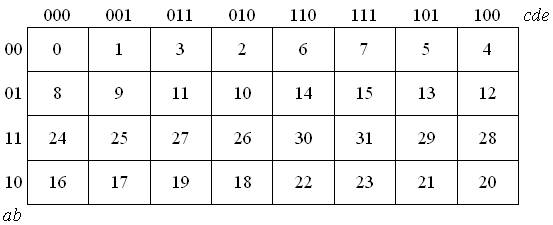
Tablica dla pięciu zmiennych:

Tablica dla sześciu zmiennych:

Diagramów Karnaugh używa się do wielu rzeczy. Przede wszystkim do minimalizacji funkcji logicznych, ale także do przedstawienia skomplikowanych funkcji logicznych przy pomocy rysunku.

Minimalizacja funkcji za pomocą tablic Karnaugh

Dla minimalizacji funkcji w informatycznych elementach logicznych najczęściej jest nam dana funkcja w postaci sumy iloczynów pełnych lub sumy z iloczynami nieistotnymi. Oczywiście nie zawsze mamy zapis

f(a,b,c,d) = abcd + ab~cd + itd.,

czasami tablica jest dana poprzez tablice prawdy lub od razu przez tablice Karnaugh. Również tutaj stosuje się zapis ze znakiem sumy. Na przykład często można się spotkać z zapisem

f(a,b,c,d) = Σ(1,2,3,6) , 

co oznacza, ze funkcja jest sumą iloczynów pełnych o numerach 1,2,3,6. W tablicach Karnaugh często mamy do czynienia z iloczynami nieistotnymi. W tym zapisie iloczyny pełne nieistotne będą zapisane w sposób następujący:

f(a,b,c,d) = Σ(1,2,3,6) + Σn(5,9,12,13).

Mając daną funkcję w ten sposób należy przepisać ją do tablicy Karnaugh dla czterech zmiennych. Tam, gdzie mamy iloczyny pod znakiem "sumy" wpisujemy jedynkę, tam gdzie mamy iloczyny pod znakiem "sumy nieistotnej" wstawiamy gwiazdkę, w reszcie pól wstawiamy zera.

Minimalizacja polega na tym, by zawsze szukać w diagramie par, czwórek lub innych potęg dwójki pól, które znajdują się obok siebie, przy czym należy przyjąć, że tablica Karnaugh jest "zawijalna", to znaczy skrajne pola są sąsiadujące. Przy poszukiwaniu takich grup pól bierzemy pod uwagę tylko te pola, w których widnieją jedynki lub gwiazdki, które można potraktować jako jedynki, ponieważ nie jest istotne, jaką wartość przyjmuje funkcja dla tego iloczyny pełnego.

Następnym krokiem jest określenie, jaki adres ma całość grupy wybranej i sklejonej. Jeśli na przykład w diagramie czterech zmiennych wybierzemy grupę ośmiu elementów, to może ona mieć adres ZM lub ~ZM, gdzie ZM jest nazwą pewnej zmiennej.

Istnieje szereg zasad, według których należy wybierać elementy grup. Przede wszystkim należy pamiętać o tym, by każda jedynka była reprezentowana w jakiejś grupie. Jeżeli nie da się dołożyć jedynki do żadnej grupy, wówczas należy w rozwiązaniu podać także jej pełny adres, czyli iloczyn pełny, który jest przez nią reprezentowany. Oczywiście należy pamiętać, by nie szastać ilością grup - musi ich być jak najmniej by otrzymać funkcję o jak najmniejszym współczynniku skomplikowania. Jeśli oda nam się wybrać taki minimalny zbiór "pokrycia" diagramu, możemy uważać powstałą formułę za minimalną.

Wszystko to brzmi na pewno bardzo niejasno, dlatego najlepszym rozwiązaniem będzie obejrzenie przykładu.

Mamy funkcję logiczną

f(a,b,c,d) = Σ(0,2,3,4,8,10,11,12).

Na razie bez iloczynów nieistotnych. Odpowiadający jej diagram będzie wyglądał następująco:

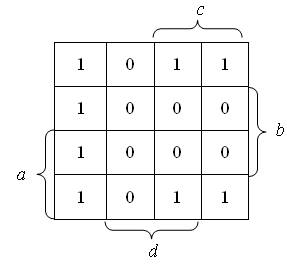
Teraz naszym zadaniem jest odnalezienie elementów sąsiadujących ze sobą w grupach po dwa, cztery lub osiem. Ósemek nie mamy, mamy za to dwie czwórki:

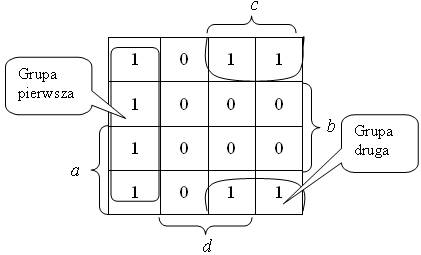
Pamiętajmy, że skrajne elementy też są sąsiadujące, dlatego grupę numer dwa można było stworzyć właśnie w taki sposób. Teraz należy określić adresy zaznaczonych grup.

Grupa pierwsza znajduje się zarówno w pasie zmiennej ~c oraz w pasie zmiennej ~d. Dlatego adres tej grupy będzie ~c~d.

Grupa druga leży na przecięciu pasów ~b oraz c, dlatego jej adresem będzie ~bc.

W ten sposób otrzymaliśmy formułę funkcji:

f(a,b,c,d) = ~bc + ~c~d.

Przeanalizujmy teraz jeszcze jeden przykład, tym razem z uwzględnieniem iloczynów nieistotnych.

Przypuśćmy, że mamy funkcję

f(a,b,c,d) = Σ(0,2,3,8,10,11) + Σn(6,7,13,14,15).

Odpowiadający tej funkcji diagram będzie wyglądał tak:

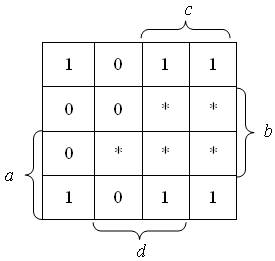
Teraz należy odnaleźć jak największe sąsiadujące grupy czwórek, ósemek czy par. Pamiętamy o tym, że iloczyny nieistotne można uznać za jedynki albo za zera, dlatego mogą być elementami grup:

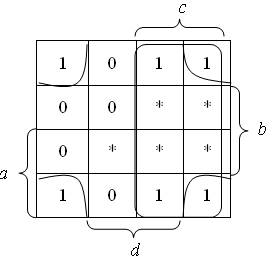
Pierwsza grupa to sąsiadujące ze sobą rogi tablicy (gdyby tablicę zwinąć w torus, te rogi by się stykały). Drugą grupę stanowi ósemka złożona z czterech jedynek oraz z czterech gwiazdek oznaczających iloczyny nieistotne. Weźmy pod uwagę, że jedna z gwiazdek została na zewnątrz wszystkich grup, zatem uznaliśmy ją za zero. Adresy tych grup to odpowiednio ~b~d dla rogów oraz c dla ósemki. Funkcja została, zatem zminimalizowana i otrzymała formułę

f(a,b,c,d) = c + ~b~d.