1. Na ładunek poruszający się w polu magnetycznym działa siła Lorenza:
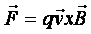
gdzie: q - ładunek
v - wektor prędkości
B - wektor indukcji magnetycznej
2. Pole magnetyczne działa również na zamknięty obwód z prądem. Przykładem może być prostokątna ramka, przez którą płynie prąd. Pojawia się wypadkowy moment sił działający na ramkę:
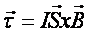
gdzie I - natężenie prądu, S - wektor powierzchni.
Wielkość 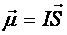 nazywa się magnetycznym momentem dipolowym.
nazywa się magnetycznym momentem dipolowym.
Pole magnetyczne działa więc na ramkę z prądem momentem skręcającym równym:
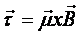
Ramkę z prądem można traktować jak dipol magnetyczny. Energia potencjalna takiego dipola jest równa:
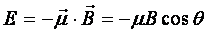
Ze wzoru wynika, że energia osiąga wartość minimalną w sytuacji gdy moment dipolowy jest równoległy do d wektora B.
3. Prawo Ampere'a
Prawo to podaje zależność między natężeniem prądu a polem magnetycznym.
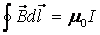
gdzie I- natężenie prądu , 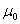 to przenikalność magnetyczna próżni.
to przenikalność magnetyczna próżni.
Ponieważ zazwyczaj nie mamy do czynienia z próżnią ale z ośrodkiem dlatego należy ten fakt uwzględnić we wzorze wprowadzając względną przenikalność magnetyczną ośrodka 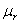 .
.
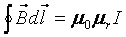
Prawo to pozwala znaleźć pole magnetyczne wytwarzane np. przez przewodniki z prądem.
Przykładowe rozkłady pól magnetycznych:
- przewodnik prostoliniowy
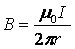
gdzie r - odległość od środka przewodnika
- solenoid
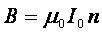
gdzie: n- liczba zwojów
I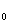 - natężenie prądu przepływającego przez pojedynczy zwój cewki
- natężenie prądu przepływającego przez pojedynczy zwój cewki
- dwa równoległe przewodniki
Dwa równoległe przewodniki zostały umieszczone w próżni w odległości d od siebie.
Przewodnik a wytwarza wokół siebie pole magnetyczne, które w odległości d jest równe:
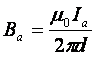
Ponieważ w tej odległości d znajduje się przewodnik b tak więc będzie na niego działała siła równa:
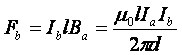
gdzie: l - odcinek przewodnika b,
I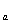 - natężenie prądu w przewodniku a,
- natężenie prądu w przewodniku a,
I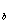 - natężenie prądu w przewodniku b
- natężenie prądu w przewodniku b
4. Prawo Biota - Savarta
Jest użyteczne do obliczania pola B w sytuacji gdy nie jest znana symetria pola. Należy wówczas podzielić przewodnik z prądem na nieskończenie małe elementy dl i obliczyć pole od każdego takiego elementu w danym punkcie.
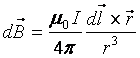
Jest to równanie wektorowe. Skalarnie natomiast można zapisać:
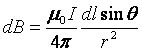
gdzie r to odległość między elementem dl a punktem dla którego obliczana jest wartość pola B.
Wypadkową indukcję magnetyczną od wszystkich elementów dl otrzymuje się przez całkowanie powyżej przedstawionego równania.
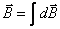
5. Prawo Gaussa dla magnetyzmu
Strumień pola magnetycznego przez powierzchnię S można obliczyć z zależności:
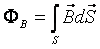
Ponieważ linie pola magnetycznego są liniami zamkniętymi tak więc strumień pola magnetycznego przez zamkniętą powierzchnie będzie równy zero.
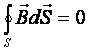
Prawo to jest bezpośrednio związane z faktem, że w przyrodzie ni stwierdzono istnienia pojedynczych biegunów magnetycznych.
6. Prawo indukcji Faradaya
Powstawanie siły elektromotorycznej indukcji czyli SEM w obwodzie pod wpływem pola magnetycznego w wyniku względnego ruchu obwodu i źródła pola nosi nazwę indukcji elektromagnetycznej.
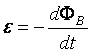
Siłą elektromotoryczna 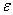 jest równa szybkości zmian strumienia magnetycznego
jest równa szybkości zmian strumienia magnetycznego 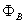 .
.
Siła elektromotoryczna może być również indukowana przez zmiany natężenia prądu płynącego w obwodzie. Zmienia się wówczas również strumień, który przechodzi przez obwód.
Zjawisko to nosi nazwę indukcji własnej, a indukowana siła to siła elektromotoryczna samoindukcji.
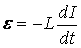
gdzie: L - współczynnik samoindukcji
I - natężenie prądu


