Wstęp:
Siła elektromotoryczna ogniwa (SEM, e) jest to wielkość fizyczna oznaczająca różnicę napięć, jaką wytwarza źródło prądu. SEM jest to napięcie panujące w obwodzie otwartym, czyli takim, w którym nie płynie prąd.
Opór elektryczny (R), to wielkość fizyczna określająca przeciwdziałanie przepływowi prądu elektrycznego przez dany materiał. Jeżeli z materiału wykonamy element zwany opornikiem, to jego opór jest równy iloczynowi napięcia na oporniku i natężenia prądu przepływającego przez ten opornik. Zależnie od tego, jaki jest obwód elektryczny, istnieją różne rodzaje oporów elektrycznych. Opór elektryczny czynny (opór omowy, rezystancja, R) występuje w obwodach prądu stałego. Opór elektryczny bierny (reaktancja, X) występuje w obwodach elektrycznych prądu przemiennego o częstości w, w który jest włączona indukcyjność (L, opór elektryczny indukcyjny, tzw. induktancja, X = wL) lub pojemność (C, opór elektryczny pojemnościowy, tzw. kapacitancja, X = 1/wC). Jeżeli obwód elektryczny zawiera zarówno rezystor, indukcyjność oraz pojemność, to mówimy o występowaniu oporu elektrycznego pozornego (impedancja elektryczna, Z = R + jX, j2 = -1 to jednostka urojona, X - wypadkowy opór bierny).
Doświadczenie:
Podczas doświadczenia wykonywaliśmy pomiary oporu wewnętrznego zasilacza, który generuje prąd stały w zakresie 2 - 3,5 A. Do doświadczenia użyto następującego obwodu elektrycznego:
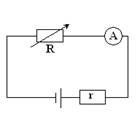
Doświadczenie polega na ustaleniu oporu na opornicy dekadowej, następnie włączeniu obwodu i ustaleniu wartości natężenia na około 2A. Następnie należy zwiększać opór na opornicy dekadowej i zapisywać zmiany natężenia prądu.
Opór wewnętrzny obliczymy stosując II prawo Kirchoffa dla obwodu zamkniętego:
e - Ir = IR
gdzie e - siła elektromotoryczna ogniwa, r - opór wewnętrzny ogniwa, R - opór zewnętrzny (opornica dekadowa) oraz I - natężenie prądu.
Prawo Kirchoffa możemy przekształcić do postaci
e = I (R + r)
Mając pomiar natężenia dla dwóch różnych wielkości oporu, możemy napisać układ równań:
e = I1(R1 + r)
e = I2(R2 + r)
Po porównaniu obu stron dostaniemy równanie:
I1(R1 + r) = I2(R2 + r)
z jedną niewiadomą - r. Z równania można wyliczyć r:
r = (I2R2 - I1R1)/(R1 - R2)
Jeżeli zmierzymy około 10 punktów I(R), to możemy wyliczyć wartość r dla kilku par punktów a następnie policzyć średnią i błąd pomiarowy.
Wykonanie pomiarów: - połączenie obwodu według schematu
- ustalenie początkowej wartości R
- zwiększanie R i odczytywanie natężenia prądu
- wykonanie obliczeń
- policzenie błędów pomiarowych
W tabeli umieszczono wyniki pomiarów:
|
R [W]
|
I [A]
| |
|
1
|
1
|
1,68
|
|
2
|
2
|
1,13
|
|
3
|
3
|
0,88
|
|
4
|
5
|
0,59
|
|
5
|
7
|
0,45
|
|
6
|
8
|
0,39
|
|
7
|
10
|
0,33
|
|
8
|
22
|
0,16
|
Obliczenia oporu wewnętrznego:
I
r = (I2R2 - I1R1)/(I1 - I2)
r = 1,1 W
II
r = (I3R3 - I1R1)/(I1 - I3)
r = 1,2 W
III
r = (I5R5 - I3R3)/(I3 - I5)
r = 1,18 W
IV
r = (I8R8 - I6R6)/(I6 - I8)
r = 1,7 W
V
r = (I8R8 - I7R7)/(I7 - I8)
r = 1,29 W
Wyniki obliczeń umieszczono w tabelce i policzono ich średnią:
|
r [W]
| |
|
1
|
1,1
|
|
2
|
1,2
|
|
3
|
1,18
|
|
4
|
1,7
|
|
5
|
1,29
|
|
Średnia
|
1,29
|
Mając policzoną średnią można policzyć średni błąd pomiarowy. Liczymy go ze wzoru
Dr = (|r1 - rśr| + |r2 - rśr| + |r3 - rśr| + |r4 - rśr| + |r5- rśr|)/5
Po podstawieniu wartości otrzymujemy wynik
Dr = 0,16
Dr/rśr = 0,12 = 12%
Otrzymaliśmy bardzo dużą wartość błędu, pewnie dlatego, że pomiary zostały wykonane niedokładnie (jedna z wartości jest wyraźnie za duża).
Wnioski z doświadczenia:
- za pomocą prawa Kirchoffa można wyznaczyć opór wewnętrzny zasilacza
- błędy pomiarowe wynikają ze złego odczytu z mierników


