Logika binarna
Logika binarna (zwana też dwuwartościową) używa operacji logicznych i posługując się zmiennymi binarnymi opisuje przetwarzanie informacji. Zmienne oznacza się literami alfabetu A, B, ...., x, y, z i nazywa literałami. Każda ze zmiennych może przyjmować tylko dwie wartości: 0 lub 1.
W logice binarnej funkcjonują trzy główne operacje logiczne: AND, OR i NOT
- operacja AND przedstawiana jest przy pomocy kropki, która jest często pomijana i odczytywana "i"
- operacja OR przedstawiana jest przy pomocy znaku "+" i odczytywana jako "lub"
- operacja NOT przedstawiana jest przy pomocy znaku prim i odczytywana jako "nie"
Definicje powyższych operatorów są określane przez tzw. tablice prawdy
- AND ( i )
|
x
|
y
|
x*y
|
|
0
|
0
|
0
|
|
0
|
1
|
0
|
|
1
|
0
|
0
|
|
1
|
1
|
1
|
- OR ( lub )
|
x
|
y
|
x+y
|
|
0
|
0
|
0
|
|
0
|
1
|
1
|
|
1
|
0
|
1
|
|
1
|
1
|
1
|
- NOT ( nie )
|
x
|
x'
|
|
0
|
1
|
|
1
|
0
|
Za pomocą zmiennych i podstawowych operacji logicznych (zwanych funktorami) możliwe jest tworzenie wyrażeń bardziej skomplikowanych, np.:
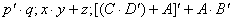
Kolejność wykonywania operatorów w wyrażeniach przedstawia się następująco:
- nawiasy
- nie
- i
- lub
Algebra Boole'a
Logika binarna jest równoważna dwuelementowej algebrze boolowskiej: 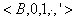 , gdzie B={0,1} oraz: działania
, gdzie B={0,1} oraz: działania 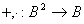 i
i 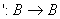 są określone prezentowanymi tablicami prawdy, odpowiednio OR, AND i NOT.
są określone prezentowanymi tablicami prawdy, odpowiednio OR, AND i NOT.
0 i 1 stanowią symbole identycznościowe dla "+" oraz "∙".
x + 0 = 0 + x = x
x ∙ 1 = 1 ∙ x = x
działania "+" oraz "∙" są łączne i przemienne
działania "+" oraz "∙" są rozdzielne jedno względem drugiego
Element x' nazywany jest dopełnieniem elementu x oraz:
x + x' = 1; x ∙ x' = 0
Z aksjomatów wynikają również inne własności algebry boolowskiej, np.:
x + x = x; x ∙ x = x;
x + 1 = 1; x ∙ 0 = 0;
(x')' = x;
Prawa DeMorgana:
(x ∙ y)' = x' + y'
(x + y)' = x' ∙ y'
x + x ∙ y = x; x ∙ (x + y) = x
znak "∙" jest pomijany w zapisie
Funkcje boolowskie
- Funkcja
![]() jest funkcją boolowską n zmiennych, np.:
jest funkcją boolowską n zmiennych, np.:
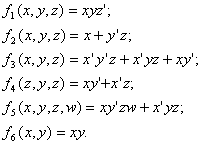
- Każda funkcja boolowska może być przedstawiona za pomocą tablic prawdy
- Dla czterech pierwszych podanych wyżej funkcji tablice przedstawiają się następująco:
|
x
|
y
|
z
|
f1
|
f2
|
f3
|
f4
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
- Dwie funkcje boolowskie są sobie równe, jeżeli posiadają takie same wartości dla każdej kombinacji zmiennych binarnych, więc:
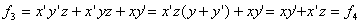
Podstawy przetwarzania informacji
Poszczególne bloki komputerów składają się z układów logicznych zwanych cyfrowymi. Nazwa ta zawiera zarówno nieskomplikowane układy małej skali integracji czyli przerzutniki i bramki oraz bardziej skomplikowane jak rejestry czy sumatory, a także układy najbardziej złożone wielkiej lub bardzo wielkiej skali integracji takie jak pamięci (VLSI i LSI) i procesory. Każdy układ logiczny może być przedstawiony jako "czarna skrzynka" (blok) z zaznaczoną odpowiednia ilością wejść oraz wyjść. Sygnały wejścia-wyjścia są sygnałami binarnymi, a opis zależności formalnych pomiędzy nimi możliwy jest dzięki algebrze Bool'a.
Aby możliwe było przetwarzanie dyskretnej informacji w formie binarnej, maszyna cyfrowa musi posiadać rejestry, czyli układy przechowujące informacje powstałe w wyniku obliczeń i wprowadzane do maszyny cyfrowej oraz cyfrowe układy logiczne, służące do manipulowania oddzielnymi bitami informacji.
Cyfrowe układy logiczne
Słowo wejściowe to uporządkowany ciąg wartości wszystkich sygnałów wejściowych określonego bloku, natomiast słowo wyjściowe to taki sam ciąg dotyczący sygnałów wyjściowych. Działanie takiego układu opisywane jest zależnością pomiędzy zbiorami słów wejściowych i wyjściowych
Wśród cyfrowych układów logicznych wyróżnia się dwa ich rodzaje:
1. Układy kombinacyjne
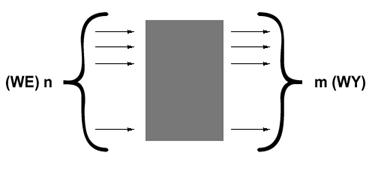
Określonemu słowu na wejściu odpowiada tylko jedno słowo na wyjściu, czyli wynik (WY) jest zależny tylko i wyłącznie od tego, co zostało podane na wejściu (WE).
Najważniejszymi czynnościami, które wykonują maszyny cyfrowe są operacje arytmetyczne. Operacje na cyfrach binarnych, jako wynik mogą dać liczbę, która składa się z dwóch cyfr. Bit, który umiejscowiony jest na bardziej znaczącej pozycji wyniku nazywany jest przeniesieniem. Jeżeli liczba zawiera więcej niż jedną cyfrę znaczącą, przeniesienie będące sumą dwóch danych bitów, dodawane jest do kolejnej, bardziej znaczącej pary. Cyfrowy układ kombinacyjny, który dodaje dwa bity nazywa się półsumatorem, a układ, który dodaje trzy bity (dwa znaczące i jeden przeniesienia) - sumatorem.
2. Układy sekwencyjne
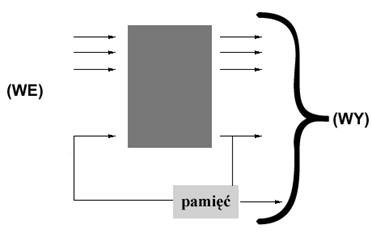
Układy sekwencyjne oprócz wykorzystania logicznych układów, wykorzystują również elementy pamięciowe. Wyjście takiego układu zależne jest nie tylko od wejścia, ale również od stanu elementów pamięciowych, stanowiących funkcję poprzednich stanów wejściowych. W efekcie sposób zachowania się takiego układu opisywany jest przy pomocy sekwencji czasowych wejść oraz stanów wewnętrznych. Nazwa "sekwencyjny" bierze się z faktu, że dla określonej sekwencji wejściowej, generowana jest dana sekwencja wyjścia. Mówi się, że układ sekwencji zapamiętuje swe stany.
Rozróżnia się dwa typy układów sekwencyjnych: asynchroniczne oraz synchroniczne. W systemach komputerowych częściej występują układy synchroniczne gdyż ich pewność działania jest większa
Działanie układów synchronicznych polega na zmianie swojego stanu i przez to stanu swoich wyjść, tylko w pewnych momentach, określanych przez generator nazywany zegarem. Mówi się, że działanie tych układów synchronizuje zegar. Układy asynchroniczne zmieniają swoje stany i stany swych wyjść podczas zmiany sygnałów na wejściach. Najczęściej spotykanymi standardowymi układami sekwencyjnymi są liczniki i rejestry.
Układy kombinacyjne
Każdy układ kombinacyjny da się określić za pomocą funkcji 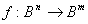 , gdzie B = {0,1}, n - ilość wejść, m- ilość wyjść
, gdzie B = {0,1}, n - ilość wejść, m- ilość wyjść
Pojedyncze wyjście układu opisuje funkcja 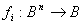 , i = 1,2, ..., m
, i = 1,2, ..., m
Układ o jednym wyjściu:
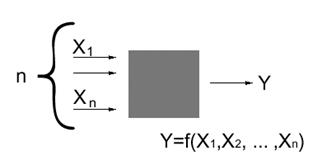
Najprostszymi układami o jednym wyjściu są bramki logiczne, odpowiadające danym operacjom logicznym:
- koniunkcji (AND)
- negacji (NOT)
- alternatywie (OR)
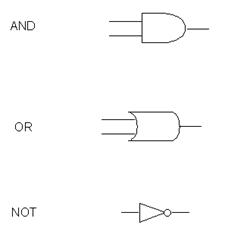
Bramki
Bramki AND, NOT i OR umożliwiają zbudowanie dowolnego układu logicznego. Występują bramki w wersjach dwu- i więcej wejściowych. Bramki elektroniczne realizowane są w różnych technologiach, stosując określone rozwiązania układów elektronicznych. Najbardziej rozpowszechnioną technologią jest CMOS, którą charakteryzuje mała moc jaką pobiera ze źródła oraz duża szybkość pracy.
Ze względów ekonomicznych, lepsza do realizacji jest funkcja boolowska postaci 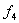 , ponieważ wymaga ona mniej wejść i bramek niż funkcja
, ponieważ wymaga ona mniej wejść i bramek niż funkcja 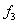 .W celu otrzymania prostszych, a co za tym idzie, tańszych układów logicznych niezbędna jest znajomość tworzenia prostych wyrażeń które opisują funkcje boolowskie. Nie ma sposobów, które zawierają w sobie wszystkie możliwe kryteria minimalizacji, do których zaliczyć można:
.W celu otrzymania prostszych, a co za tym idzie, tańszych układów logicznych niezbędna jest znajomość tworzenia prostych wyrażeń które opisują funkcje boolowskie. Nie ma sposobów, które zawierają w sobie wszystkie możliwe kryteria minimalizacji, do których zaliczyć można:
- zredukowanie liczby połączeń i elementów
- obniżenie czasu propagacji
- ograniczenia obciążeń
Najczęściej sposób upraszczania zależny jest od zastosowań danego układu oraz od umiejętności projektanta.
Nazwy bramek wzięły się od słów z języka angielskiego AND, NOT, OR i oznaczają:
- NAND - not and (nie i) - negacja iloczynu logicznego
- XOR exclusive or (suma wyłączająca), oznaczana czasami EXOR
- NOR - not or (nie lub) - negacja sumy logicznej
Postać normalna funkcji boolowskiej
W funkcji boolowskiej dwóch zmiennych (x i y), każda zmienna może przybierać postać zanegowaną lub zwykłą, dlatego istnieją 4 kombinacje:
xy, x'y, xy', x'y' - dla iloczynu
x+y, x'+y, x+y', x'+y' - dla sumy
Iloczyny nazywane są mintermami, sumy zaś - makstermami. W sytuacji, gdy występuje n zmiennych, również określa się makstermi i mintermi, a jest ich wtedy 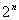
Każdy minterm otrzymuje się w następujący sposób: zmienne, dla których na określonej pozycji liczny binarnej jest 0 są zanegowane, natomiast zmienne, dla których występuje 1 nie są zanegowane
Każdy maksterm otrzymuje się w następujący sposób: zmienne, dla których na określonej pozycji liczny binarnej jest 1 są zanegowane, natomiast zmienne, dla których występuje 0 nie są zanegowane
Przykład, gdzie n = 3
|
mintermy
|
makstermy
| |||
|
x
|
y
|
z
|
składnik
|
czynnik
|
|
0
|
0
|
0
|
x'y'z'
|
x+y+z
|
|
0
|
0
|
1
|
x'y'z
|
x+y+z'
|
|
0
|
1
|
0
|
x'yz'
|
x+y'+z
|
|
0
|
1
|
1
|
x'yz
|
x+y'+z'
|
|
1
|
0
|
0
|
xy'z'
|
x'+y+z
|
|
1
|
0
|
1
|
xy'z
|
x'+y+z'
|
|
1
|
1
|
0
|
xyz'
|
x'+y'+z
|
|
1
|
1
|
1
|
xyz
|
x'+y'+z'
|
Każda funkcja boolowska, może zostać przestawiona jako wyrażenie algebraiczne na podstawie tej tablicy prawdy, poprzez utworzenie minitermu dla każdego układu zmiennych, dla którego funkcja przyjmuje wartość 1, a następnie poprzez złączenie wszystkich składników przy pomocy operacji OR.
Podobnie, każda funkcja boolowska może być zaprezentowana w postaci iloczynu (AND) makstermów. Tworzy się makstermy dla każdego układu zmiennych, dla którego funkcja przyjmuje wartość 0, a następnie łączy się je przy pomocy operacji AND.
Ta istotna wartość algebry Boole'a mówi, że dowolna funkcja boolowska może zaprezentowana jako suma mintermów lub iloczyn makstermów.
Funkcja boolowska ma postać normalną, jeżeli jest przedstawiona w postaci sumy iloczynów zawierających dowolna ilość literałów, np.:
x' + xy + xz' + xyz,
x(y'+z)(x+y+z')
Minimalizacja funkcji boolowskiej
Jednym z algorytmów upraszczającym funkcję boolowską jest metoda tablic Karnaugh, dostarczająca prostej metody minimalizacji liczby zmiennych występujących w funkcji. Jeżeli postać wyrażenia algebraicznego jest mniej złożona, automatycznie pociąga to za sobą mniejszą złożoność układu cyfrowego.
Tablice dla dwóch oraz trzech zmiennych.
W przypadku dwóch zmiennych, występują cztery mintermy. Przedstawia je poniższa tabela.
|
y
| |||
|
0
|
1
| ||
|
x
|
0
|
x'y'
|
x'y
|
|
1
|
xy'
|
xy
| |
W przypadku trzech zmiennych, ilość mintermów wynosi osiem. Przedstawia to poniższa tabela.
|
yz
| |||||
|
00
|
01
|
11
|
10
| ||
|
x
|
0
|
x'y'z'
|
x'y'z
|
x'yz
|
x'yz'
|
|
1
|
xy'z'
|
xyz'
|
xyz
|
xyz'
| |
Mintermy są tak zorganizowane, by sąsiadujące pola różniły się od siebie tylko jedną zmienną, która jest zanegowana w jednym polu, a w drugim nie (sąsiednimi są również skrajne pola, tak jakby tablica była rozrysowana ścianie walca). Jak wynika z własności algebry boolowskiej, suma dwóch mintermów z sąsiadujących pól może zostać uproszczona do postaci pojedynczego składnika iloczynowego, który składa się z dwóch zmiennych.

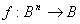 jest funkcją boolowską n zmiennych, np.:
jest funkcją boolowską n zmiennych, np.:
