- Kwantowe własności promieniowania elektromagnetycznego.
Pod koniec XIX wieku fizyka wydawała się być nasycona już nowoodkrytymi prawami rządzącymi przyrodą i całym Wszechświatem. Uczeni nie spodziewali się już wielkich nowości w swojej dziedzinie. Jednak już rok 1900 i koleje lata przyniosły wiele zaskakujących i wręcz fenomenalnych odkryć. Zapoczątkowały one powstanie i gwałtowny rozwój nowej dziedziny - fizyki kwantowej. Jako jej początek przyjmuje się datę 14 grudnia 1900 roku, kiedy to Max Planck postawił hipotezę, że energia światła nie jest ciągła, ale jest wysyłana i pochłaniania małymi porcjami. Porcje te zostały nazwane kwantami. Mając na uwadze tę własność, Planck zauważył, że energia promieniowania ciała doskonale czarnego nie może być zupełnie dowolna, ale powinna wyrażać się jako wielokrotność kwantu energii. Własność tę nazwano kwantowością.
Max Planck określił wzór na energię kwantu promieniowania elektromagnetycznego:
E = h ∙ V,
gdzie:
V- częstotliwość promieniowania
h - stała Plancka= 6,62∙10-34J∙s
A następnie korzystając z hipotezy kwantowości wyprowadził wzór na widmową zdolność emisyjną ciała doskonale czarnego:
Rλ=(2∙π∙c2∙h) / [λ5∙(eh∙c/k∙λ∙T-1)],
gdzie:
h- stała Plancka
k - stała Boltzmana
c - prędkość światła
T - temperatura w skali bezwzględnej
2. Prawo przesunięć Wiena.
Prawo to zostało sformułowane na bazie doświadczeń przez Wilhelma Wiena w roku 1893. Dotyczy ono promieniowania elektromagnetycznego emitowanego przez ciało doskonale czarne. Wien stwierdził w nim, że wzrostowi temperatury ciała doskonale czarnego, towarzyszy przesunięcie zakresu widma jego promieniowania w kierunku fal krótszych. Przesunięcie to nazywane jest przesunięciem Wiena i wyraża się wzorem:
Λmax = b/T
Λmax - długość fali o największym nasileniu promieniowania
B -stała Wiena o wartości 2,8977685 ∙ 10-3 +/- 5,1 ∙10-9 m∙K
T - temperatura ciała doskonale czarnego
Przesunięcie Wiena jest obserwowane jako zmiana koloru wysyłanego promieniowania. Przykładowo: weźmy pod uwagę ciało czarne, np. kulkę z żelaza i poddawajmy ją działaniu coraz wyższej temperatury. Oto co zaobserwujemy: kulka najpierw nie będzie emitować światła, w temperaturze ok. 8000K zacznie świecić kolorem żaru - ciemnoczerwonym, po kolejnym wzroście temperatury, kulka zmienia kolory od pomarańczu przez żółty i fioletowy. Jeśli weźmiemy do pomocy pryzmat, to zauważymy że dodatkowo kulka emituje jeszcze dwie fale niewidoczne gołym okiem. Przed ciemnoczerwoną fala podczerwieni, a poza fioletem fala nadfioletu.
Zjawisko przesunięć Wiena jest wspaniałym narzędziem do badania temperatur np. gwiazd, oczywiście przy założeniu, ze traktujemy jako ciała doskonale czarne.
Prawo Wiena zostało sformułowane wcześniej niż tzw. rozkład Plancka (różnica 7 lat), ale jest traktowane jako wniosek z tegoż rozkładu.
3. Zjawisko fotoelektryczne (fotoemisja elektronowa).
Zjawisko fotoelektryczne zewnętrzne polega na wybiciu elektronów z powierzchni ciała stałego pod wpływem padającego promieniowania. Zjawisko to zależy od rodzaju substancji, na którą pada promieniowanie oraz jego częstotliwości. Wyemitowane elektrony nazywamy fotoelektronami. Najlepsze efekty przynosi promieniowanie fali o małej długości (czyli dużej częstotliwości) skierowane na metal. Pierwszym naukowcem, który matematycznie wyjaśnił to zjawisko był Albert Einstein, za co został nagrodzony Nagrodą Nobla w roku 1921. Einstein przyjął zgodnie z teorią Plancka, że promieniowanie padające na dany np. metal ma postać kwantów - fotonów, o energii E = h∙V każdy. Stwierdził również, że energia padających fotonów nie jest zamieniana tylko na energię kinetyczną (rozpędzenie) wybijanych z metalu elektronów, ale również na tzw. pracę wyjścia. Jest to praca wykonana nad elektronami jeszcze w metalu - potrzebna do wyrwania ich z jego powierzchni. Praca wyjścia zależy bezpośrednio od rodzaju substancji biorącej udział w zjawisku. Dlatego też z niektórych substancji łatwiej jest wyrwać elektrony, a z innych trudniej. Wzór Alberta Einsteina wyjaśniający zjawisko fotoelektryczne zewnętrzne wygląda następująco:
h∙V = W + Ek,
gdzie:
h - stała Plancka (jak wyżej)
V - częstotliwość fali promieniowania
W -praca wyjścia
Ek - energia kinetyczna uwolnionych z metalu elektronów.
Oprócz zjawiska fotoelektrycznego zewnętrznego istnieje też zjawisko fotoelektryczne wewnętrzne. Zachodzi ono w półprzewodnikach, a polega ono na tym, że: gdy naświetlamy półprzewodnik promieniowaniem elektromagnetycznym o odpowiedniej częstotliwości, to powoduje to przeniesienie nośników ładunku elektrycznego w przewodniku (elektronów swobodnych lub tzw. "dziur") na wyższy poziom energetyczny. Efektem jest wzrost przewodnictwa w półprzewodniku.
2. Fale de Broglie'a - fale materii.
Podstawą do odkrycia fal de Broglie'a stała się hipoteza założona w 1900 roku przez M. Plancka o korpuskularno - falowej (cząsteczkowo - falowej) budowie promieniowania elektromagnetycznego (tzn, że np. światło można traktować jako falę i jako materię zbudowana z pewnych cząstek tzw. fotonów). W roku 1924 uczony Louis de Broglie na podstawie teoretycznych rozważań stwierdził, że taką właśnie podwójną budowę ma również materia. Rozszerzając swe przewidywania Broigle założył, że długość przewidywalnych fal emitowanych przez cząstki materii (o niezerowym pędzie) powinna być określona związkiem, nazywanym wzorem de Broglie'a:
λ = h/p,
gdzie:
λ - długość fali materii
h - stała Plancka
p - pęd cząstki materii.
Podobnie również, zgodnie z teorią fali każdej cząstce o energii E można przypisać inną charakteryzującą ją wielkość - częstotliwość υ:
f = E/h.
Wielka hipoteza L. de Broglie'a spotkała się z ogromnym zainteresowaniem i poparciem. W roku 1927 została potwierdzona doświadczalnie (sprawdzenie, czy fale materii ulegają podobnie jak inne fale zjawisku dyfrakcji i interferencji), a w roku 1929 jej odkrywca został nagrodzony Nagrodą Nobla.
- Zasada nieoznaczoności Heisenberga.
Zasada ta została sformułowana przez Wernera Heisenberga w 1927 i jest bardzo ważną teorią fizyki kwantowej. Dotyczy również korpuskularno - falowej budowy materii. Zasada nieoznaczoności mówi, że nawet z największą dokładnością nie można jednocześnie wyznaczyć pędu i położenia danej cząstki.
Jeżeli przyjmiemy oznaczenia:
∆x - nieokreśloność pomiaru położenia
∆p - nieokreśloność pomiaru pędu
h - stała Plancka,
ħ - stała Diraca o wartości h/2
to zasadę nieoznaczoności Heisenberga możemy określić wzorem:
∆x∙∆p ≥ h/(4∙ π)=ħ/2
W roku 1945 Leonid Mandelshtam i Igora Tamma uzasadnili, że zasada nieoznaczoności Heisenberga odnosi się również do energii cząstek (a dokładnie energii jej fali de Broglie'a) i czasu jej życia:
∆E∙∆t ≥ħ
Istotny jest fakt, ze zasada nieoznaczoności obowiązuje nie tylko w mikroświecie, ale i w makroświecie. Nieoznaczoność pomiaru prowadzonego w mikroświecie może nam się kojarzyć z błędem pomiaru. A wartość ta nie jest błędem, ale oszacowaniem "obszaru" najbardziej prawdopodobnych wyników pomiaru. I to niezależnie od tego, czy pomiar prowadzony jest przy użyciu narzędzi bardzo dokładnych, czy też narażonych na pewien błąd pomiaru. W otaczającym nas makroświecie nieoznaczoność pomiarów jest mniej istotna ze względu na to, że małe wahania wyników "giną" w porównaniu ze skala samego wyniku.
2. Równanie Schrodinger'a i jego zastosowanie.
Odkrycie fal de Broglie'a zapoczątkowało rozwój fizyki kwantowej. Erwin Schrodinger wykorzystując przyjęte przez Plancka i Broglie'a wzory określające częstotliwość υ i długość fali materii λ: ν = E/h, λ = h/p (gdzie: p - pęd cząstki, h - stała Plancka), zdefiniował całkowitą energię cząstki:
E = p2/2mo + V,
gdzie:
p -pęd cząstki,
m0 - masa spoczynkowa cząstki
V - energia potencjalna cząstki
Zastanawiał się również nad tym, że jeśli potraktujemy elektron jako falę, to nie będzie możliwe dokładne określenie miejsca, w którym się znajduje ta cząstka. Schrodinger doszedł do wniosku, że jedyne co można zrobić, to obliczyć prawdopodobieństwo, że dany elektron jest w przyjętym punkcie. W tym celu sformułował słynne równanie, tzw. równanie Schrodingera. Wyraża ono ruch cząstki pod wpływem działającej na nią siły (elektromagnetyczna, grawitacyjna, itp.) z prędkością dużo mniejszą od prędkości światła. Cząstką tą może być zarówno elektron lub dowolna inna cząstka, której znamy masę. Rozwiązanie równania Schrodingera (jest to równanie różniczkowe) dla konkretnej cząstki określa jakich fal może być ona źródłem. Rozwiązanie to nazywamy tzw. funkcją falową, jest ona zależna od czasu i położenia, a oznacza się ją: Ψ(x, y, z, t).
Ogólna postać równania Schrodingera jest dosyć skomplikowana i wygląda następująco:
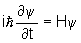
gdzie:
i - jednostka urojona,
ħ = h/2π - stała Diraca
(h - stała Plancka),
t - czas,
H - hamiltonian układu
ψ - funkcja falowa opisująca ten układ.
Kwadrat modułu (wartość bezwzględna) wartości funkcji falowej ψ określa gęstość prawdopodobieństwa znalezienia cząstki w danym miejscu (proporcjonalnie do wartości). Trzeba również pamiętać, że niepewność położenia cząstki w danym miejscu nie może być mniejsza niż określa to zasada nieoznaczoności Heisenberga.
2. Zasada Pauliego i układ okresowy pierwiastków.
Zakaz Pauliego to prawo sformułowane przez Wolfganga Pauliego w 1925, będące jego wnioskiem obserwacji nad widmami atomowymi poszczególnych pierwiastków. Zakaz Pauliego mówi, że dowolne dwa elektrony w atomie nie mogą znajdować się w tym samym stanie kwantowym, czyli muszą się różnić tzw. liczbą kwantową. Wprowadzając ten zakaz, Pauli wyjaśnił przyczyny niesamowitych regularności w widmach atomowych. Stał się on również podstawą do odkrycia wielu innych prawidłowości w chemii i fizyce. Jedną z najbardziej znanych i chyba najważniejszych jest zależność budowy orbit elektronów w atomach od własności fizyko-chemicznych pierwiastków. Co to oznacza? Jak wiemy elektrony krążą wokół jądra atomu, po kilku orbitach (o różnym stopniu energii). Zakaz Pauliego nie pozwala na przebywanie na jednej orbicie więcej niż dwóch elektronów o tym samym spinie (momencie pędu). Dzięki temu elektrony rozmieszczane są na orbitach według zasady - po zapełnieniu pierwszej orbity zgodnie z zakazem Pauliego, następne elektrony przechodzą na drugą, i ponownie dopiero po jej zapełnieniu na trzecią, itd. Dzięki temu mamy ogromną różnorodność pierwiastków. Bo gdyby wszystkie z nich posiadały elektrony upakowane wyłącznie na pierwszej orbicie, to mielibyśmy do czynienia jedynie z gazami doskonałymi i nie byłoby możliwości zachodzenia przemian chemicznych. Zakaz Pauliego jest podstawowym prawem uzasadniającym słuszność budowy okresowego układu pierwiastków, gdyż bardzo jasno określa budowę orbit w atomach ilość krążących po nich elektronów, a to z kolei pozwala na dokładne sklasyfikowanie z jakiego pierwiastka pochodzi dany atom.
Układ okresowy pierwiastków.
Układ okresowy pierwiastków to tabela przedstawiająca zestawienie wszystkich pierwiastków, uporządkowanych według rosnącej liczby atomowej (ilości elektronów w wolnym atomie, lub protonów w jądrze atomu), a także pogrupowanych w zależności od własności fizyko-chemicznych. Takie graficzne ułożenie pierwiastków umożliwia bardzo łatwo i szybko rozróżniać ich właściwości w zależności od położenia w układzie. Tabela układu okresowego (według Wernera) składa się z siedmiu wierszy zwanych okresami i osiemnastu kolumn zwanych grupami. (Najnowsze opracowania układu okresowego liczą już 8, a nawet 9 okresów). Grupy zawierają pierwiastki o jednakowej ilości elektronów na powłokach zewnętrznych/walencyjnych i dzielimy je na: główne (numeracja cyframi rzymskimi od I do VIII) i poboczne (w których graficznie oddzielone są dwie grupy lantanowców i aktynowców). Natomiast okresy ponumerowane są cyframi arabskimi od 1 do 7, a numer okresu określa ilość powłok elektronowych w danym pierwiastku. "Okresowość" w nazwie układu pierwiastków wynika z faktu, że w grupach głównych (przechodząc poziomo od I do VIII) co 8 pierwiastków następuje zapełnienie jednej orbity elektronami i przeskok następnych elektronów na wyższą orbitę. W taki właśnie cykliczny sposób tworzone są kolejne orbity w atomach i stąd wzięło się w układzie pierwiastków wyróżnienie tych o jednakowej ilości powłok w osobnym wierszu (poziomie).
Rozmieszczenie pierwiastków w układzie według grup pozwala zauważyć jeszcze jedną prawidłowość. Grupa I i II (z wyłączeniem wodoru), to pierwiastki silnych metali. Wraz z przemieszczeniem się do dalszych grup (poziomo od I do VIII) zauważamy wyraźne słabnięcie własności metalicznych, poprzez metale przejściowe, lantanowce, aktynowce i metaloidy, aż do silnych niemetali i w końcu gazów szlachetnych. Oznacza to, że jeśli rozważamy każdą grupę osobno (jako kolumnę), to im niżej znajduje się w niej pierwiastek, tym jest lepszym metalem. W przypadku niemetali - wraz z wysokością w kolumnie spada "siła" niemetalu. Natomiast wszystkie atomy grup pobocznych, a także lantanowce i aktynowce to metale, ale w ich obrębie wewnętrzny podział na silniejsze i słabsze nie jest już tak regularny jak w grupach głównych.
Najdziwniejszy jest fakt, że twórca pierwszego układu okresowego pierwiastków Dmitrij Mendelejew, prawidłowo porozmieszczał wszystkie znane mu pierwiastki, bazując jedynie o ich masy atomowe. Opublikował go w roku 1869, a układ ten dzisiaj znany jako tablica Mendelejewa lub krótka forma układu okresowego pierwiastków, zawierał już ponad 90 pierwiastków. Wspaniałym pomysłem uczonego było również, to że nie zakładał iż znane są już wszystkie pierwiastki i ż jego układ musi być pozbawiony luk. Tam gdzie zaobserwował zbyt duże różnice w masach atomowych lub własnościach chemicznych pozostawiał puste miejsca. W kolejnych latach nowo odkryte pierwiastki idealnie pasowały do układu i wykazywały właściwości chemiczne zgodne z umiejscowieniem w układzie. W roku 1905 Alfred Werner opierając się na układzie Mendelejewa stworzył jego dłuższą formę, która jest nadal najczęściej używana. Powstanie pierwszych układów okresowych pierwiastków, było w znacznym stopniu intuicyjnym i obserwacyjnym "układaniem puzzli", o nie znanym wyglądzie całości. Naukowym potwierdzeniem tej "fizyko-chemicznej układanki" stały się takie wydarzenia, jak: odkrycie jądra atomowego przez Rutherforda (1911), tabela liczby protonów i elektronów w pierwiastkach (Moseley, rok 1913), budowa atomu ogłoszona przez Bohra, a przede wszystkim Zakaz Pauliego (1925r.), który wyjaśnił pochodzenie własności chemicznych pierwiastków.
Obecnie nadal uzupełnia się układ okresowy pierwiastków o kolejne nowoodkryte. Została również delikatnie zmieniona jego struktura graficzna. Zatwierdzaniem nowych pierwiastków, ich nazw i symboli zajmuje się międzynarodowa organizacja IUPAC.


